
6.若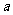 为实数,则“
为实数,则“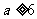 ”是“关于
”是“关于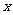 的方程
的方程 有实数解”的(
)
有实数解”的(
)
A.必要而不充分条件 B.充分而不必要条件
C.充要条件 D.既不充分也不必要条件
5.一袋中装有大小相同,编号分别为 的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为 ( )
的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为 ( )
A.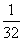 B.
B.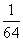 C.
C.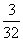 D.
D.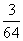
4.下列函数中,在区间(0,2)上为增函数的是 ( )
A. B.
B.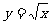 C.
C.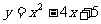 D.
D.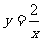
3.若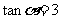 ,
,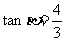 ,则
,则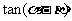 = ( )
= ( )
A. B.
B. C.
C.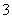 D.
D.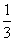
2.某物体运动的位移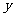 (单位:m)是时间
(单位:m)是时间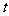 (单位:s)的函数
(单位:s)的函数 ,当
,当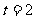 s时,物体的瞬时速度
s时,物体的瞬时速度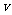 等于 ( )
等于 ( )
A.15m/s B.18m/s C.19m/s D.20m/s
1.若集合 ,则
,则 ( )
( )
A.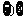 B.
B.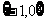 C.
C.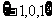 D.
D.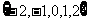
22.(本小题满分14分)袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是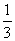 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ)从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.(i)求恰好摸5次停止的概率;(ii)记5次之内(含5次)摸到红球的次数为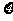 ,求随机变量
,求随机变量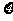 的分布率及数学期望E
的分布率及数学期望E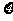 .
.
(Ⅱ)若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是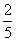 ,求p的值.
,求p的值.
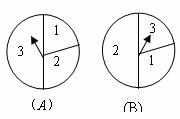
21.(本小题满分14分)如图所示, 有两个独立的转盘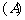 、
、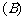 两个图中三个扇形区域的圆心角分别为
两个图中三个扇形区域的圆心角分别为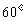 、
、 、
、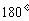 .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘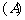 指针对的数为
指针对的数为 ,转盘
,转盘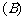 指针对的数为
指针对的数为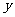 .设
.设 的值为
的值为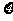 ,每转动一次则得到奖励分
,每转动一次则得到奖励分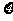 分
分
(1)求 <2且
<2且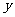 >1的概率;
>1的概率;
(2)某人玩12次,求他平均可以得到多少奖励分?
20.(本小题满分12分)二项式 展开式中第五项的二项式系数是第三项系数的4倍。求:(1)n ;(2)展开式中的所有的有理项。
展开式中第五项的二项式系数是第三项系数的4倍。求:(1)n ;(2)展开式中的所有的有理项。
19.某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 种.(用数字作答).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com