
4.设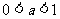 ,函数
,函数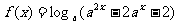 ,则使
,则使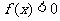 的
的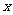 的取值范围是 。
的取值范围是 。
3.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积和侧面积之比为 。
2. 。
。
1.已知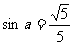 ,则
,则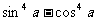 的值为 。
的值为 。
20.(本小题满分16分)
已知数列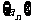 中的相邻两项
中的相邻两项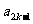 ,
,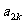 是关于
是关于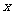 的方程
的方程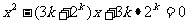 的两个根,且
的两个根,且 1,2,3,…).
1,2,3,…).
(1)求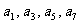 ;
;
(2)求数列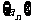 的前2n项和S
的前2n项和S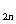 。;
。;
(3)记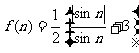 ,
,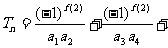
 …
…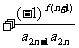 ,求证:
,求证: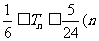 ∈N*).
∈N*).
19.(本小题满分15分)
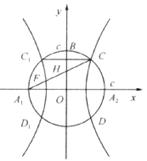
如图,以A1,A2为焦点的双曲线E与半径为c的圆O相交于C,D,C1,D1,连接CC1与OB归交于点H,且有: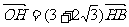 .其中A1,A2,B是圆O与坐标轴的交点,c为双曲线的半焦距.
.其中A1,A2,B是圆O与坐标轴的交点,c为双曲线的半焦距.
(1)当c=1时,求双曲线E的方程;
(2)试证:对任意正实数c,双曲线E的离心率为常数;
(3)连接A1C与双曲线E交于F,是否存在实数 ,使
,使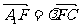 恒成立?若存在,试求出
恒成立?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
18.(本小题满分15分)
已知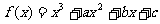 有极大值
有极大值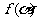 和极小值
和极小值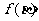 .
.
(1)求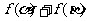 的值;
的值;
(2)设曲线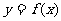 的极值点为A、B,求证:线段AB的中点在
的极值点为A、B,求证:线段AB的中点在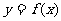 上.
上.
17.(本小题满分15分)
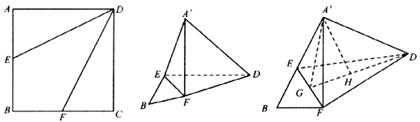
正方形ABCD中,AB=2,E是AB边的中点,F是BC边上一点,将△AED及△DCF折起(如图),使A、C点重合于A’点.
(1)证明:A’D⊥EF;
(2)当F为BC的中点时,求A’D与平面DEF所成的角;
(3)当BF=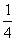 BC时,求三棱锥A’-EFD的体积.
BC时,求三棱锥A’-EFD的体积.
16.(本小题满分15分)
近年来,太阳能技术运用的步伐日益加快.2002年全球太阳电池的年生产量达到670兆瓦,年生产量的增长率为34%.以后四年中,年生产景的增长率逐年递增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦);
(2)目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
15.(本小题满分14分)
已知函数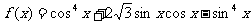 .
.
(1)求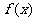 的最小正周期;
的最小正周期;
(2)若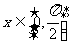 ,求
,求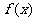 最大值、最小值。
最大值、最小值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com