
6.如图是一个空间几何体的三视图,根据图中尺寸(单位:cm),可知几何体的表面积是
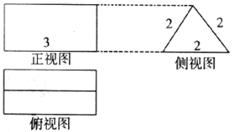
A.(18+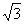 )cm2 B.(16+2
)cm2 B.(16+2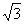 )cm2
)cm2
C.(17+2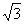 )cm2 D.(18+2
)cm2 D.(18+2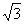 )cm2
)cm2
5.已知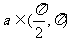 ,
,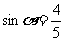 ,则
,则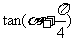 等于
等于
A.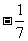 B.7 C.
B.7 C.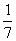 D.-7
D.-7
4.“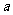 =2”是函数
=2”是函数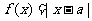 在区间[2,+∞)上为增函数的
在区间[2,+∞)上为增函数的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
3.若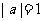 ,
,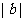 =2,
=2,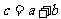 ,<
,<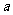 ,b>=120°,则<
,b>=120°,则<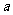 ,
,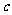 >等于
>等于
A.60° B.90° C.120° D.150°
2.已知S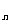 是等差数列{
是等差数列{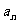 }的前
}的前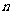 项和,且S13=35+S8,则S21的值为
项和,且S13=35+S8,则S21的值为
A.1 B.146 C.147 D.148
1.已知集合A={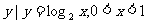 },B={
},B={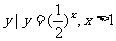 },则下列结论正确的是
},则下列结论正确的是
A.A∩B=A B.A∪B=B C.(CRA)∩B=A D.(CRA)∩B=B
20.(本题满分14分)
已知二次函数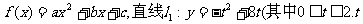 为常数);
为常数);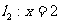 .若直线
.若直线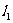 、
、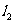 与函数
与函数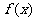 的图象以及
的图象以及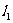 、
、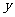 轴与函数
轴与函数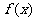 的图象所围成的封闭图形如阴影所示.
的图象所围成的封闭图形如阴影所示.
(Ⅰ)求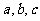 的值
的值
(Ⅱ)求阴影面积S关于t的函数S(t)的解析式;
(Ⅲ)若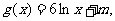 问是否存在实数m,使得
问是否存在实数m,使得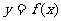 的图象与
的图象与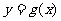 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.

19.(本题满分12分)
现有甲、乙两个盒子,甲盒子里盛有4个白球和4个红球,乙盒子里盛有3个白球和若干个红球.若从乙盒子里任取两个球,取到同色球的概率是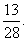
(Ⅰ)求乙盒子里红球的个数;
(Ⅱ)若从甲盒子里任意取出两个球,放入乙盒子里充分搅拌均匀后,再从乙盒子里任意取出2个球放回甲盒子里,求甲盒子里的白球没有变化的概率.
18.(本题满分12分)
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
17.(本题满分12分)
已知函数 的图像过点
的图像过点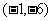 ,且函数
,且函数 的图象的对称轴为
的图象的对称轴为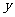 轴
轴
(I)求函数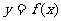 的解析式及它的单调递减区间
的解析式及它的单调递减区间
(II)若函数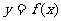 的极小值在区间
的极小值在区间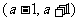 内,求
内,求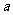 的取值范围
的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com