
7. 不等式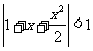 的解集是( )
的解集是( )
A.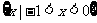 B.
B.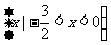
C.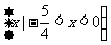 D.
D.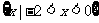
6.将红、黑、白三个棋子放入如图所示的小方格内,每格只能放一个棋子且三个棋子既不同行也不同列,则不同放棋子的方法有( )

A. 576种 B.288种 C.144种 D.96种
5.在每一试验中事件A发生的概率均为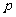 ,则在
,则在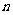 次试验中
次试验中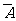 恰好发生
恰好发生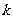 次的概率为
( )
次的概率为
( )
A.1-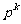 B.
B.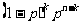 C.1-
C.1-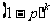 D.
D.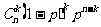
4.设随机变量ζ服从二项分布B(n,p),且Eζ=1.6 Dζ=1.28,则 ( )
A.n=4 ,p=0.4 B. n=8, p=0.2 C. n=5,p=0.32 D. n=7,p=0.45
3.若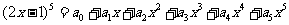 ,则
,则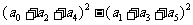 的值是( )
的值是( )
A.243 B.-243 C.64 D.-64
2.已知随机变量ζ服从正态分布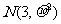 ,且P(ζ<2)=0.3 则P(2<ζ<4)的值等于( )
,且P(ζ<2)=0.3 则P(2<ζ<4)的值等于( )
A.0.5 B.0.2 C.0.3 D.0.4
1.9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的种数是( )
A.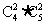 B.
B.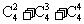
C.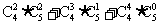 D.
D.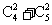
22.(本题满分14分)
已知函数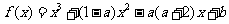
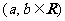 .
.
(I)若函数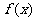 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求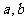 的值;
的值;
(II)若函数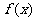 在区间
在区间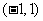 上不单调,求
上不单调,求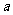 的取值范围.
的取值范围.
21.(本小题满分12分)
已知二次函数 f(x)= x 2 – 4 x – 4 在闭区间 [ t , t + 1 ] (t ∈R )上的最小值记为g(t).
(1)试写出g(t )的函数表达式;
(2)作g(t )的大致图象,并写出g(t )的最小值。(不要求证明)
20.(本小题满分12分)
围建一个面积为360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口,如图所示。已知旧墙的维修费用为45元/m, 新墙的造价为180元/m, 设利用的旧墙的长度为x ( 单位:m ), 修建的总费用为 y (单位:元 )。
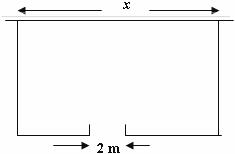
(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x值, 使修建此矩形场地围墙的总费用最小,并求出最小总费用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com