
2、复数(3+i)m-(2+i)对应的点在第三象限内,则实数m的取值范围是 ( )
A.m< B.m<1 C.<m<1 D.m>1
1、已知全集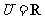 ,集合
,集合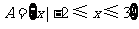 ,
,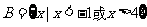 ,那么集合
,那么集合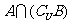 等于 ( )
等于 ( )
A.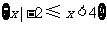 B.
B.
C.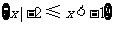 D.
D.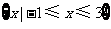
(17) (本小题满分10分)
已知△ABC的内角A、B、C所对的边分别为a,b,c,且a=2, cosB=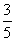 .
.
(1)若b=4,求sinA的值;
(2)若△ABC的面积S△ABC=4,求b,c的值.
(18)(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为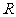 的函数:
的函数:
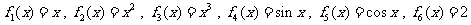 .
.
(Ⅰ)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数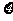 的分布列和数学期望。
的分布列和数学期望。
(19)(本小题满分12分)
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,D、E、F分别是棱PA、PB、PC的中点,连接DE,DF,EF.
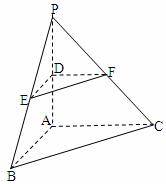
(1)求证: 平面DEF∥平面ABC;
(2)若PA=BC=2,当三棱锥P-ABC的体积的最大值时,求二面角A-EF-D的平面角的余弦值.
(20)(本小题满分12分)
某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成. 每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N*)
(1)设完成A 型零件加工所需时间为f(x)小时,写出f(x)的解析式;
(2)为了在最短时间内完成全部生产任务,x应取何值?
(21)(本小题满分12分)
已知椭圆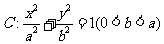 的离心率为
的离心率为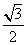 ,且经过点
,且经过点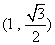
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存在经过点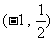 的直线
的直线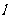 ,它与椭圆
,它与椭圆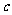 相交于
相交于 两个不同点,且满足
两个不同点,且满足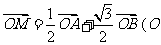 为坐标原点)关系的点
为坐标原点)关系的点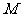 也在椭圆
也在椭圆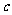 上,如果存在,求出直线
上,如果存在,求出直线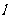 的方程;如果不存在,请说明理由。
的方程;如果不存在,请说明理由。
(22)(本小题满分12分)
已知数列{an}的相邻两项an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,且a1=1.
(1)求证:数列{
an-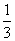 ×2n}是等比数列;
×2n}是等比数列;
(2)设Sn是数列{an}的前n项的和,问是否存在常数λ,使得bn-λSn>0对任意n∈N*都成立,若存在,求出λ的取值范围;若不存在,请说明理由.
(1)已知全集 ,集合
,集合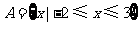 ,
,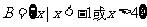 ,那么集合
,那么集合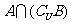 等于
等于
A.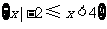 B.
B.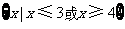
C.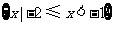 D.
D.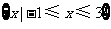
(2)复数(3+i)m-(2+i)对应的点在第三象限内,则实数m的取值范围是
A.m< B.m<1 C.<m<1 D.m>1
(3)直线 与圆
与圆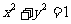 的位置关系是
的位置关系是
A.相离 B.相交 C.相切 D.不确定
(4)已知p:关于x的不等式x2+2ax-a>0的解集是R,q:-1<a<0,则p是q 的那么
A.充分非必要条件 B.必要非充分条件
C. 充要条件 D.既非充分又非必要条件
(5)某校举办奥运知识竞赛,有6个代表队参赛,每队有2名学生,若12名参赛同学中有4人获奖,且这4人来自3个不同的代表队,则不同的获奖种数共有
A.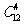 B.
B.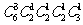 C.
C.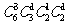 D.
D.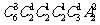
(6)在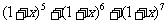 的展开式中,含
的展开式中,含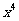 项的系数是通项公式为
项的系数是通项公式为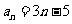 的数列
的数列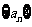 的
的
A.第3项 B.第11项 C.第20项 D.第24项
(7)对于下列命题
①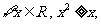 ②
②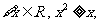 ③
③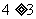 ;
;
④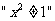 的充要条件是
的充要条件是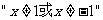 。
。
其中正确命题的个数是
A.0 B.1 C.2 D.3
(8)函数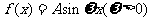 ,对任意
,对任意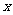 有
有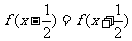 ,且
,且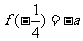 ,那么
,那么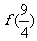 等于
等于
A.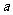 B.
B.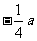 C.
C.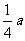 D.
D.
(9)若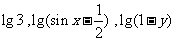 顺次成等差数列,则
顺次成等差数列,则
A.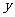 有最大值1,无最小值
B.
有最大值1,无最小值
B.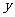 有最小值
有最小值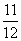 ,无最大值
,无最大值
C.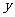 有最小值
有最小值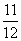 ,最大值1
D.
,最大值1
D.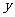 有最小值
有最小值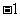 ,最大值1
,最大值1
(10)在 中,
中,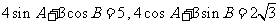 ,则角
,则角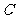 等于
等于
A.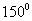 B.
B.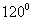 C.
C. D.
D.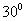
(11)在平面直角坐标系 中,设直线
中,设直线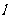 与抛物线
与抛物线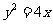 相交于
相交于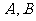 两点,给定下列三个条件:①
两点,给定下列三个条件:①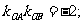 ②
②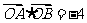 ; ③直线
; ③直线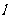 过定点(2,0)。如果将上面①、②、③中的任意一个作为条件,余下两个作为结论,则构成的三个命题中,真命题的个数是
过定点(2,0)。如果将上面①、②、③中的任意一个作为条件,余下两个作为结论,则构成的三个命题中,真命题的个数是
A.3 B.2 C.1 D.0
(12)已知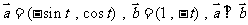 ,则
,则 的值为
的值为
A.1 B.0 C.5 D.8
22.(本小题满分14分)
若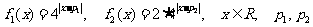 为常数,且
为常数,且
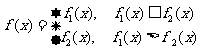
(1)求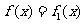 对所有实数x成立的充要条件(用p1.p2表示)
对所有实数x成立的充要条件(用p1.p2表示)
(2)设a、b为两个实数 a<b,且p1.p2∈(a, b),若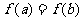 ,
,
在(1)的条件下求证: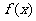 在区间[a, b]上的单调递增区间的长度为
在区间[a, b]上的单调递增区间的长度为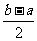 (闭区间[a, b]的长度定义为︱b –a︱)
(闭区间[a, b]的长度定义为︱b –a︱)
21.(本小题满分12分)
甲有一个盒子,里面装有x个红球,y个白球(x≥0,y≥0,且x +y=4);乙有一个盒子,里面装有2个红球,1个白球,1个黄球。现在甲从盒子里任取2个球,乙从盒子里任取1个球,若取出的3个球颜色全不相同,则甲获胜。
(1)试问甲如何安排盒子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的平均数。
20.已知直线 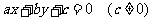 与圆
与圆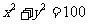 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
A.56条 B.68条 C.72条 D.78条
19.设函数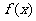 是定义在
是定义在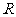 上的且以3为周期的奇函数,若
上的且以3为周期的奇函数,若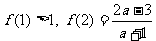 ,则( )
,则( )
A.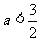 B.
B.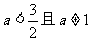 C.
C.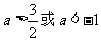 D.
D.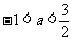
18.如图,它满足 ①第n行首尾两数均为n,②表中的递推关系类似杨辉三角,则第n行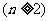 第2个数是_______.
第2个数是_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com