
23.(本题满分10分)坐标系与参数方程选做题
已知曲线 、
、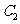 的极坐标方程分别为
的极坐标方程分别为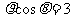 ,
,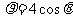
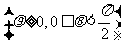 ,求曲线
,求曲线 、
、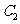 交点的极坐标.
交点的极坐标.
22.(本题满分10分)不等式选讲选做题
已知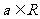 ,若关于
,若关于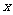 的方程
的方程 有实根,求
有实根,求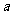 的取值.
的取值.
21.(本题满分12分)已知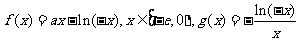 其中
其中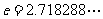 是自然对数的底数,
是自然对数的底数,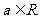
(1)若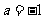 ,求
,求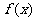 的极值;
的极值;
(2)求证:在(1)的条件下,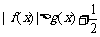 ;
;
(3)是否存在实数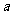 ,使
,使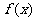 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出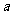 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
请考生在第22,23两题中任选一题做答,写出必要解答过程,如果多做,则按所做的第一题计分
20.(本题满分12分)一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转速度而变化,下表为抽样试验的结果:
|
转速x(转/秒) |
16 |
14 |
12 |
8 |
|
每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(1)利用散点图或相关系数r的大小判断变量y对x是否线性相关?为什么?
(2)如果y与x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?
(最后结果精确到0.001.参考数据: ,
,
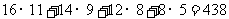 ,
,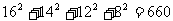 ,
,
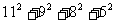 =291).
=291).
19.(本题满分12分) 某商场准备在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电商品、4种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品至少有一种日用商品的概率;
(2)商场对选出的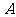 商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高180元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等概率的.
商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高180元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等概率的.
 请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
18.(本题满分12分)袋中有20个大小相同的球,其中记上0号的有10个,记上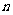 号的有
号的有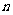 个(
个( ).现从袋中任意取一球,
).现从袋中任意取一球,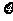 表示所取球的标号.
表示所取球的标号.
(1)求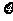 的分布列、期望和方差;
的分布列、期望和方差;
(2)若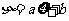 ,
,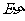 =1,
=1,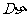 =11,试求
=11,试求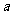 、
、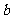 的值。
的值。
17.(本题满分12分)已知p:|1-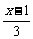 |≤2,q:x2-2x+1-m2≤0(m>0),若
|≤2,q:x2-2x+1-m2≤0(m>0),若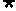 p是
p是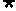 q的必要而不充分条件,求实数m的取值范围.
q的必要而不充分条件,求实数m的取值范围.
16.已知定义域为 的函数
的函数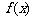 对任意实数
对任意实数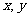 满足
满足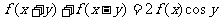 ,且
,且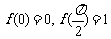 .给出下列结论:①
.给出下列结论:①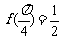 ,②
,②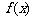 为奇函数,③
为奇函数,③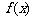 为周期函数,④
为周期函数,④ 内单调递减.其中,正确的结论序号是
.
内单调递减.其中,正确的结论序号是
.
15.已知抛物线的对称轴在y轴的左侧,其中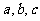 ∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=“
∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=“ 的取值”,则X的均值EX为______.
的取值”,则X的均值EX为______.
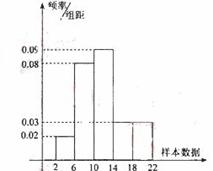
14.下图是样本容量为200的频率分布直方图。 根据样本的频率分布直方图估计,样本数据落在(2,10)内的频率约为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com