
20.(本题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=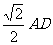
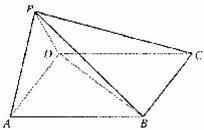
(I)求证:平面PDC⊥平面PAD;
(Ⅱ)求二面角B-PD-C的余弦值.
19.(本题满分12分)已知函数f(x)=ax3+bx2(x∈R)的图像过点P(-1,2),且在点P处的切线恰好与直线x-3y=0垂直.
(I)求函数f(x)的解析式;
(Ⅱ)若函数f(x)在区间[m,m+1]上单调递增,求实数m的取值范围.
18.(本题满分12分)证明:当n≥3(n ∈N*)时,2n≥2(n+1)..
17.(本题满分12分)有4个不同的小球,4个不同的盒子,现要把球全部放进盒子内.
(Ⅰ)没有空盒子的方法共有多少种?
(Ⅱ)可以有空盒子的方法共有多少种?
(Ⅲ)恰有1个盒子不放球,共有多少种方法?(最后结果用数字做答)
16.将正方形ABCD沿对角线BD折成直二面角A-BD-C,如图所示,有如下四个结论:
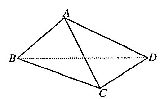
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成600角;
④AB与CD所成的角为600.其中真命题的序号是____________(写出所有真命题的序号).
15.对某种产品的5件不同正品和4件不同次品进行检测,直到区分出所有次品为止.若所有次品恰好经过五次检测被全部发现,则这样的检测方法有_____________种.(最后结果用数字做答)
14.设函数f(n)=k(其中n∈N*),k是e(其中e=2.7182828284……)的小数点后的第n位数字.例如f(6)=2.则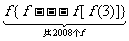 =__________________
=__________________
13.若(x-2)5=a5x5+a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4+a5=__________________.
12.已知抛物线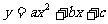 (a≠0)的对称轴在y轴的左侧,其中a、b、c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=“︱a-b︱的取值”,则X的数学期望E(x)为
(a≠0)的对称轴在y轴的左侧,其中a、b、c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=“︱a-b︱的取值”,则X的数学期望E(x)为
A.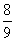 B.
B.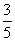 C.
C.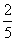 D.
D.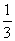
第Ⅱ卷(共90分)
11.已知至同四边形OABC,其对角线为OB,AC,M,N分别是对边OA,BC的中点,点G在线段MN上且使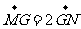 ,用基向量
,用基向量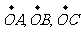 表示向量
表示向量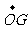 是
是
A.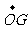 =
= B.
B.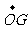 =
=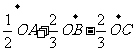
C.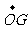 =
=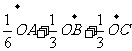 D.
D.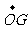 =
=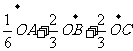
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com