
20.已知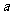 为实数,函数
为实数,函数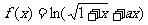 .
.
(1)证明:当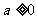 时,
时,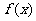 在其定义域内单调递增;
在其定义域内单调递增;
(2)求函数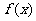 的定义域;
的定义域;
(3)求当 时,求
时,求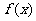 的单调减区间.
的单调减区间.
19.在经济学中,函数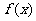 的边际函数为
的边际函数为 ,定义为
,定义为 ,某公司每月最多生产100台报警系统装置。生产
,某公司每月最多生产100台报警系统装置。生产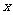 台的收入函数为
台的收入函数为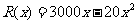 (单位元),其成本函数为
(单位元),其成本函数为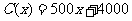 (单位元),“利润”等于“收入”与“成本”之差.
(单位元),“利润”等于“收入”与“成本”之差.
(1)求出利润函数 及其边际利润函数
及其边际利润函数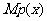 ;
;
(2)求出的利润函数 及其边际利润函数
及其边际利润函数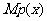 是否具有相同的最大值;
是否具有相同的最大值;
(3)你认为本题中边际利润函数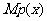 最大值的实际意义.
最大值的实际意义.
18.有八个函数,它们是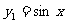 ,
,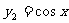 ,
,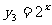 ,
,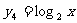 ,
,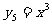 ,
, ,
,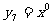 ,
,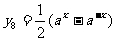 (
( 且
且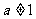 ).从这八个函数中任取出三个,求取出的这三个函数中,奇函数个数
).从这八个函数中任取出三个,求取出的这三个函数中,奇函数个数 的分布列及数学期望.
的分布列及数学期望.
17.函数 ,且
,且 .
.
(1)求实数 的值.
的值.
(2)求函数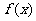 单调区间并求出所有极值.
单调区间并求出所有极值.
(3)求在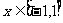 上,函数
上,函数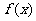 的最大与最小值.
的最大与最小值.
16.函数 ,且
,且 又
又 ,若
,若 ,则在
,则在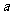 是正偶数的条件下,
是正偶数的条件下,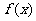 是偶函数的概率是 .
是偶函数的概率是 .
15.已知集合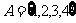 与
与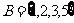 ,有一一映射
,有一一映射 ,则满足
,则满足 的映射有 个.
的映射有 个.
14.已知命题 且“
且“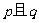 ”与“非
”与“非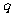 ”同时为假命题,则
”同时为假命题,则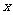 的取值集合为 .
的取值集合为 .
13.定义:在区间 中,我们把
中,我们把 叫做区间
叫做区间 的长度.函数
的长度.函数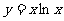 与函数
与函数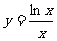
在相同的单调区间中,区间长度的最大值是 .
12.已知函数 与函数
与函数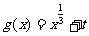 ,若
,若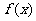 与
与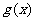 的交点在直线
的交点在直线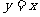 的两侧,则实数
的两侧,则实数 的取值范围是( )
的取值范围是( )
A.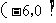 B.
B.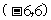 C.
C. D.
D.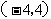
(第II卷 非选择题)
11.直线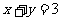 与函数
与函数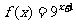 和函数
和函数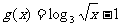 的图像交于两点的横坐标分别为
的图像交于两点的横坐标分别为 ,则
,则 的值是( )
的值是( )
A.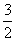 B.3 C.
B.3 C.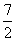 D.7
D.7
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com