
6.方程2cos2x = 1的解是 .
5.现有形状特征一样的若干个小球,每个小球上写着一个两位数,一个口袋里放有标着所有不同的两位数的小球,现任意取一个小球,取出小球上两位数的十位数字比个位数字大的概率是 .
4.向量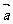 、
、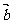 满足|
满足|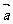 |=2,|
|=2,|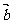 |=3,且|
|=3,且|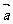 +
+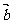 |=
|=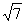 ,则
,则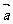 .
.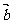 = .
= .
3.等差数列{an}中,a5+a8+ a11+ a14+ a17=50,则S21= .
2.已知f(x)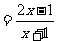 ,则
,则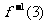 =____________.
=____________.
1.设全集U ={a、b、c、d、e}, 集合A={a、b},B={b、c、d},则A∩CUB=________.
22.(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3小题满分8分)
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f -1(x)能确定数列{bn},bn= f –1(n),若对于任意nÎN*,都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(1)若函数f(x)= 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;
(2)已知正数数列{cn}的前n项之和Sn= (cn+
(cn+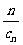 )。写出Sn表达式,并证明你的结论;
)。写出Sn表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn=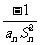 ,Dn是数列{dn}的前n项之和,且Dn>log
a (1-2a)恒成立,求a的取值范围
,Dn是数列{dn}的前n项之和,且Dn>log
a (1-2a)恒成立,求a的取值范围
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分)
设有抛物线C:y= –x2+ x–4,通过原点O作C的切线y=mx,使切点P在第一象限.
x–4,通过原点O作C的切线y=mx,使切点P在第一象限.
(1)求m的值,以及P的坐标;
(2)过点P作切线的垂线,求它与抛物线的另一个交点Q;
(3)设C上有一点R,其横坐标为t,为使DOPQ的面积小于DPQR的面积,试求t的取值范围.
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在美国广为流传的一道数学题目是:老板给你两种加工资的方案. 第一种方案是每年年末(12月底)加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加1000元;第二种方案是每半年(6月底和12月底)各加薪一次,每次所加的工资数是在上次所加工资数的基础上再增加300元,请选择一种.
根据上述条件,试问:
(1)如果你将在该公司干十年,你将选择哪一种加工资的方案?(说明理由)
(2)如果第二种方案中的每半年加300元改成每半年加a元,那么a在什么范围内取值时,选择第二种方案总是比选择第一种方案多加薪?
19.(本题满分14分)本题共有3个小题,第1小题满分4分,第2、3小题满分各5分)
已知边长为6的正方形ABCD所在平面外一点P,PD^平面ABCD,PD=8,

(1)连接PB、AC,证明:PB ^ AC;
(2)连接PA,求PA与平面PBD所成的角的大小;
(3)求点D到平面PAC的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com