
22.斜率为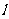 的直线过抛物线
的直线过抛物线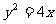 的焦点,且与抛物线交于两点
的焦点,且与抛物线交于两点 、
、 .
.
(1)求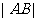 的值;
的值;
(2)将直线 按向量
按向量 =(-2,0)平移得直线
=(-2,0)平移得直线 ,
, 是
是 上的动点,求
上的动点,求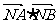 的最小值.
的最小值.
(3)设 (2,0),
(2,0),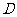 为抛物线
为抛物线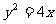 上一动点,证明:存在一条定直线
上一动点,证明:存在一条定直线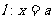 ,使得
,使得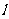 被以
被以 为直径的圆截得的弦长为定值,并求出直线
为直径的圆截得的弦长为定值,并求出直线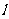 的方程.
的方程.
21.如图,在四棱锥 中,底面
中,底面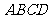 是边长为2的菱形,∠
是边长为2的菱形,∠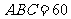 °,
°,
 ⊥平面
⊥平面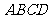 ,
,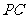 与平面
与平面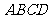 所成角的大小为
所成角的大小为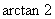 ,
, 为
为 的中点.
的中点.
(1)求四棱锥 的体积;
的体积;
(2)求异面直线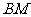 与
与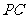 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
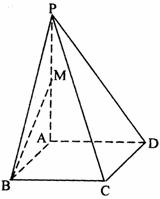
20.已知 =
= ,
, =
=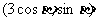 ,
, 是平面上的两个向量
是平面上的两个向量
(1)试用 、
、 表示
表示 ·
· .
.
(2)若 ·
· =
=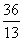 ,且
,且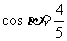 ,求
,求 的值.(结果用反三角函数值表示)
的值.(结果用反三角函数值表示)
19.设数列{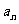 }的前
}的前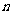 项和为
项和为 ,
,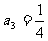 .对任意
.对任意 ,向量
,向量 ,
, 满足
满足 ⊥
⊥ ,求
,求 .
.
18.已知关于 的不等式
的不等式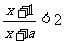 的解集为
的解集为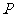 ,若
,若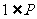 ,则实数
,则实数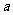 的取值范围为( )
的取值范围为( )
A. B.
B.
C. D.
D.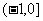
17.在实数数列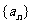 中,已知
中,已知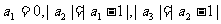 ,…,
,…,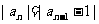 则
则
 的最大值为 ( )
的最大值为 ( )
A.0 B.1 C.2 D.4
16. 恒等于 ( )
恒等于 ( )
A. B.
B. C.
C. D.
D.
15.已知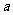 ,
,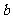 都是实数,则“
都是实数,则“ ”是“
”是“ ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
14.设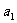 ,
, ,…,
,…,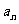 是各项不为零的
是各项不为零的 项等差数列,且公差
项等差数列,且公差 ≠0.若将数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对
≠0.若将数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对 所组成的集合为
.
所组成的集合为
.
13.已知 是1、2、
是1、2、 、4、5这五个数据的中位数,又知-1、5、
、4、5这五个数据的中位数,又知-1、5、 、
、 这四个数据的平均数为3,则
这四个数据的平均数为3,则 最小值为 .
最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com