21．(本小题满分8分)

盒中有质地大小相同的5个红球和4个黑球．

(Ⅰ)每次不放回的取一个球，求第一次第二次都取到红球的概率；

(Ⅱ)每次取一个球，记住颜色后仍放回该盒子，如此进行三次，求三次中恰有两次取到红球的概率；

(Ⅲ)从盒子中取出3个球，设三个球中红球的个数为X，求随机变量X的概率分布列．

20．(本小题满分8分)

有6个人站成一排照相．

(Ⅰ)甲乙二人相邻的排法有多少种？

(Ⅱ)甲不站在两端的排法有多少种？

(Ⅲ)这时又有2个人加入，也站在这一排照相；在不打乱原有6个人顺序的基础上，有多少种不同的加入方法？

19．某射手射击一次，击中目标的概率是p(p∈(0，1))，他连续射击k次(k≥3，k∈N)，且各次射击是否击中目标相互之间没有影响．有下列结论：

①他第3次击中目标的概率是p；

②他恰好击中目标3次的概率是；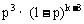

③他至少击中目标1次的概率是；

其中正确的结论序号是 　　　　　(写出所有正确结论的序号)．

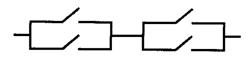
18．如图，在一段线路中并联和串联着4个常用开关，线路能否正常工作的原理与串并联电路相同．假定在某段时间内每个开关能够闭合的概率都是0.8，则这段时间内该线路能正常工作的概率为　　　　 (用数字作答)．

17．已知集合。设点，则可以组成的不同点的个数有　　　　　 .

16．计算＝　　　　 .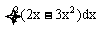

15．若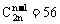，则=　　　　　 .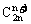

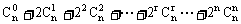14．若展开式的各项系数之和为1024，则的值为

A．2⁵　　　　　　　　　 　　 B．2¹⁰　　　　　　　　　 　 　C．3⁵　　　　　　　　　 　　 D．3¹⁰

13．将标号为1，2，3，…，8的8个球，放入标号为1，2，3，…8的8个盒子内，每个盒子内放入一个球，恰好有3个球的标号与其所在盒子的标号不一致的放入方法种数为

A．56　　 　　　　　　 　　B．112　　 　　　　　 　　C．168　 　　　　　　　 　　D．336

12．若由一个2×2列联表中的数据计算得到，那么　　

A．有95%的把握认为这两个变量有关系

B．有95%的把握认为这两个变量存在因果关系

C．有99%的把握认为这两个变量有关系

D．没有充分的证据显示这两个变量之间有关系