21．(本小题满分13分)

已知二次函数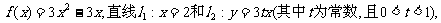

直线l₂与函数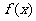的图象以及直线l₁、l₂与函数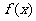的图象所围成的封闭图形如图中阴影所示，设这两个阴影区域的面积之和为

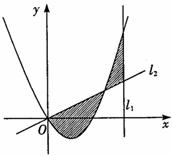
　 (I)求函数的解析式；

　 (II)定义函数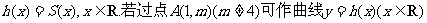的三条切线，求实数m的取值范围。

20．(本小题满分13分)

　　　　 已知椭圆中心在原点，焦点在x轴上，离心率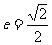，过椭圆的右焦点且垂直于长轴的弦长为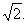

　 (I)求椭圆的标准方程；

　 (II)已知直线l与椭圆相交于P、Q两点，O为原点，且OP⊥OQ。试探究点O到直线l的距离是否为定值？若是，求出这个定值；若不是，说明理由。

19．(本小题满分13分)

为了保护三峡库区的生态环境，凡是坡度在25°以上的坡荒地都要绿化造林。据初步统计，到2004年底库区的绿化率只有30%。计划从2005年开始加大绿化造林的力度，每年原来坡度在25°以上的坡荒面积的16%将被造林绿化，但同时原有绿化面积的4%还是会被荒化。设该地区的面积为1，2004年绿化面积为，经过一年绿化面积为a₂，…，经过n年绿化面积为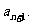

　 (I)试写出的关系式，并证明数列是等比数列；

　 (II)问至少需要经过多少年努力，才能使库区的绿化面积超过60%？

18．(本小题满分12分)

　　　　 如图，在三棱锥P-ABC中，PA=PB=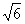，PA⊥PB，AB⊥BC，∠BAC=30°，平面PAB⊥平面ABC。

　 (I)求证：PA⊥BC；

　 (II)求二面角P-AC-B大小的正切值。

17．(本小题满分12分)

　　　　 为了收集2009年7月“长江日全食”天象的有关数据，国家天文台在成都、武汉各设置了A、B两个最佳观测站，共派出11名研究员分别前往两地实地观测。原计划向成都派出3名研究员去A观测站，2名研究员去B观测站；向武汉派出3名研究员去A观测站，3名研究员去B观测站，并都已指定到人。由于某种原因，出发前夕要从原计划派往成都的5名研究员中随机抽调1人改去武汉，同时，从原计划派往武汉的6名研究员中随机抽调1人改去成都，且被抽调的研究员仍按原计划去A观测站或B观测站工作。求：

　 (I)派往两地的A、B两个观测站的研究员人数不变的概率；

　 (II)在成都A观测站的研究员从数X的分布列和数学期望。

16．(本小题满分12分)

已知函数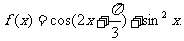

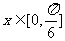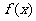　 (I)当时，求函数的值域；

　 (II)在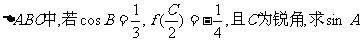的值。

15．给出如下定理：“若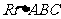的斜边AB上的高为h，则有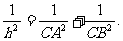”在空间四面估P-ABC中，若PA、PB、PC两两垂直，底面ABC上的高为h，类比上述定理，得到的正确结论是　　　　　　　　 。

14．已知曲线C的参数方程是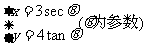，则曲线C的离心率为　　　 ；若点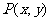在曲线C上运动，则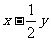的取值范围是　　　　　 。

13．已知点O为=　　　 。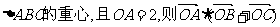

12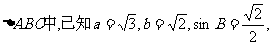．则符合此条件的三角形有　　 个。