
1.函数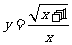 的定义域为( )
的定义域为( )
A.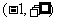 B.
B. C.
C.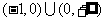 D.
D.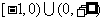
20.(本题满分16分)
设函数f(x)= x3-mx2+(m2-4)x,x∈R.
(1)当m=3时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)已知函数f(x)有三个互不相同的零点0,α,β,且α<β.若对任意的x∈[α,β],
都有f(x)≥f(1) 恒成立,求实数m的取值范围.
19.(本题满分16分)
已知:在数列{an}中,a1= ,an+1= an+.
(1)令bn=4n an,求证:数列{bn}是等差数列;
(2)若Sn为数列{an}的前n项的和,Sn+λnan≥ 对任意n∈N*恒成立,求实数λ的最小值.
18.(本题满分16分)
已知直线l1:3x+4y-5=0,圆O:x2+y2=4.
(1)求直线l1被圆O所截得的弦长;
(2)如果过点(-1,2)的直线l2与l1垂直,l2与圆心在直线x-2y=0上的圆M相切,圆M被直线l1分成两段圆弧,其弧长比为2∶1,求圆M的方程.
17.(本题满分14分)
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式P= ,Q= t。今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).
求:(1)y关于x的函数表达式;
(2)总利润的最大值.
16.(本题满分14分)
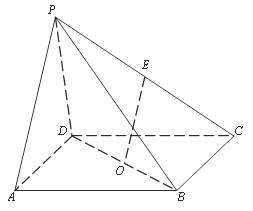
如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.
求证:(1)EO∥平面PAD;
(2)平面PDC⊥平面PAD.
15.(本题满分14分)
已知sinx= ,x∈(,π),求cos2x和tan(x+)值.
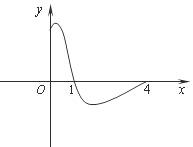
14.函数f(x)是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式 <0的解集为 .
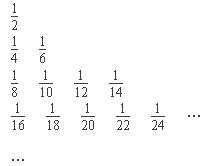
13.把数列{}的所有项按照从大到小,左大右小的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为(k,s),则 可记为 .
12.已知A(-3,0),B(0,),O为坐标原点,点C在第二象限,且∠AOC=60°,
→=λ→+→,则实数λ的值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com