
4.已知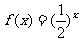 ,命题
,命题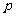 :
: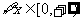 ,
,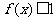 ,则 ( )
,则 ( )
A.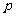 是假命题,
是假命题,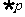 :
:
B.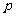 是假命题,
是假命题,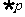 :
:
C.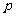 是真命题,
是真命题,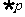 :
: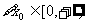 ,
,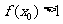
D.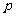 是真命题,
是真命题,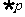 :
:
3.已知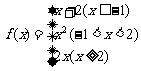 ,若
,若 ,则
,则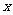 的值为 ( )
的值为 ( )
A.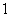 B.
B.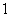 或
或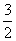 C.
C.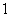 或
或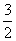 或
或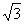 D.
D.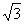
2. 已知复数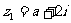 ,
,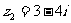 ,若
,若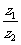 为实数,则实数
为实数,则实数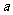 的值为 ( )
的值为 ( )
A.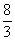 B.
B. C.
C.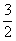 D.
D.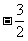
1. 设集合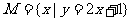 ,集合
,集合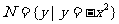 ,则 ( )
,则 ( )
A.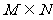 B.
B.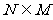 C.
C.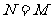 D.
D.
24.(选修4-5不等式选讲)(本小题满分10分)
设函数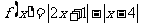 .
.
(1)求不等式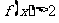 的解集;
的解集;
(2)求函数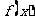 的最小值.
的最小值.
23.(选修4-4极坐标与参数方程)(本小题满分10分)
已知直线 的参数方程为
的参数方程为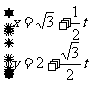 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为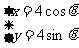 (θ为参数).
(θ为参数).
(1)将曲线C的参数方程化为普通方程;
(2)若直线l与曲线C交于A、B两点,求线段AB的长.
22.(选修4-1几何证明选讲)(本小题满分10分)
如图,圆O和圆 相交于A,B两点,AC是圆
相交于A,B两点,AC是圆 的切线,AD是圆O的切线,若BC=2,AB=4,求BD的长.
的切线,AD是圆O的切线,若BC=2,AB=4,求BD的长.

21.(本小题满分12分)已知函数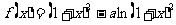 在
在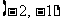 上是增函数,在
上是增函数,在 上是减函数.
上是减函数.
(1)求函数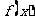 的解析式;
的解析式;
(2)若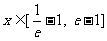 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)是否存在实数b,使得方程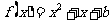 在区间
在区间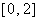 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题计分.
20.(本小题满分12分)已知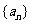 是等比数列,
是等比数列, ,
, ;
; 是等差数列,
是等差数列, ,
,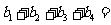
 .
.
(1)求数列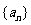 的前
的前 项和
项和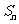 的公式;
的公式;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,
,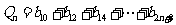 ,其中
,其中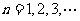 ,试比较
,试比较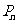 与
与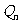 的大小,并证明你的结论.
的大小,并证明你的结论.
19.(本小题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为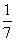 .现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止.每个球在第一次被取出的机会是等可能的,用
.现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止.每个球在第一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.
求:(1)袋中原有白球的个数;
(2)随机变量 的数学期望;
的数学期望;
(3)甲取到白球的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com