3．已知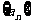是等差数列，，，则过点的直线的斜率是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．4　　　 　　 　　　　　　 B．　　 　　　　 　　 C．－4　 　　　　 　　 D．－14

2．若直线与直线互相垂直，则a的值为　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．　　 　　　　　　　　 B．　　　　　 　　　 C．　　　　 　　　　　 D．1

1．原点到直线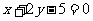的距离为　　　　　　　　　　　　　　　 　　　 　　　　　　　　　　　　 ( 　　)

A．1　　　　　　　 　　　　　　　 B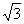．　　　　　 　　 　　　 C．2　　　　　　　 　 　　　　 D．

22．已知中，，，平面BCD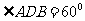，，E,F分别是AC,AD上的动点，且

(1)求证：不论为何值，总有平面平面ABC

(2)当为何值时，平面平面ACD

21．已知直三棱柱中，为等腰直角三角形，，且，分别为的中点，

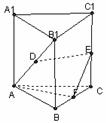
(1)求证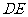：//平面；

(2)求证：平面；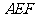

(3)求点E到平面的距离。

20．在棱长为_a的正方体中，E、F分别是棱AB和BC上的动点，且AE=BF

(1)求证：；

(2)当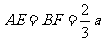时，求三棱锥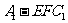的体积。

19．若奇函数f(x)在定义域(-1，1)上是减函数，

(1)求满足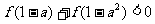的a的取值集合M；

(2)对于(1)中的a，求函数的定义域。

18．渔场中鱼群的最大养殖量为m吨，为保证鱼群的生长空间，初始实际养殖量不能达到最大养殖量，必须留出适当的空闲量．已知鱼群的年增长量y吨与空闲率和初始实际养殖量x的乘积成正比(空闲率为空闲量与最大养殖量的比值)，比例系数为k(k>0)，

(1)求鱼群年增长量y关于x的函数关系式；

(2)求鱼群年增长量的最大值。

17． 一个圆锥的底面半径为2cm，高为6cm，在其中有一个高为xcm的内接圆柱，

(1)求圆锥的表面积和体积；

(2)当x 为何值时，圆柱侧面积最大？求出最大值。

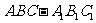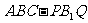16．直三棱柱中，P、Q分别是侧棱、上的点，且，则四棱锥的体积与多面体的体积的比为　　　　　　　 ．