
1.若集合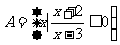 ,
,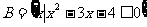 ,则
,则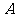
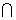 (
(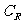
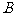 )等于 ( )
)等于 ( )
A.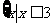 或
或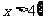 B.
B.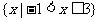
C.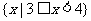 D.
D.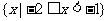
21.(13分)设函数f(x)=p(x-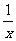 )-2lnx,g(x)=
)-2lnx,g(x)= (p是实数,e为自然对数的底数)
(p是实数,e为自然对数的底数)
(1)若f(x)在其定义域内为单调函数,求p的取值范围;
(2)若直线l与函数f(x),g(x)的图象都相切,且与函数f(x)的图象相切于点(1,0),求p的值;
(3)若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求p的取值范围.
20.(13分)已知函数f(x)=x+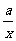 的定义域为(0,+∞)且f(2)=2+
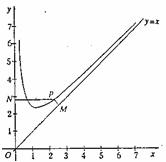
的定义域为(0,+∞)且f(2)=2+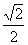 ,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N。
,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N。
(1)求a的值;
(2)问:|PM|·|PN|是否为定值?若是,则求出该定值,若不是,则说明理由:
(3)设O为坐标原点,求四边形OMPN面积的最小值。
19.(12分)
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c。
若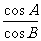 =
=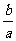 且sinC=cosA
且sinC=cosA
(1)求角A、B、C的大小;
(2)设函数f(x)=sin(2x+A)+cos(2x-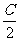 ),求函数f(x)的单调递增区间,并指出它相邻两对称轴间的距离。
),求函数f(x)的单调递增区间,并指出它相邻两对称轴间的距离。
18.(13分)某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训.已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,求这3人中至少有2人参加过培训的概率.
17.(12分) 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点
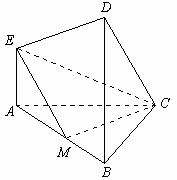
(I)求证:CM ⊥EM:
(Ⅱ)求DE与平面EMC所成角的正切值.
16.(12分)已知向量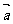 =(sin
=(sin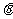 ,cos
,cos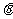 -2sin
-2sin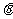 ),
), =(1,2)
=(1,2)
(1)若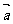 ⊥
⊥ ,求tan
,求tan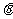 的值;
的值;
(2)若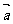 ∥
∥ ,且
,且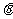 为第Ⅲ象限角,求sin
为第Ⅲ象限角,求sin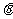 和cos
和cos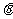 的值。
的值。
15.如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,
 ,则由图中点C在C’上方可得不等式
,则由图中点C在C’上方可得不等式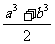 >
>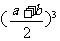 ,请分析函数y=lgx(x>0)的图象,类比上述不等式可以得到的不等式是
。
,请分析函数y=lgx(x>0)的图象,类比上述不等式可以得到的不等式是
。

14.已知f(x)在R上是奇函数,且f(4-x)= -f(x),当x∈(0,2)时,f(x)=log2(x2+15),则f(7)=
13.f(x)=(x2-3)ex(e为自然对数的底数)的最小值是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com