
2.{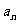 }为正项等比数列,且
}为正项等比数列,且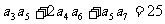 ,则
,则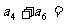
A.25 B.20 C.15 D.5
1.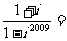
A.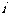 B.
B.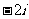 C.1 D.
C.1 D.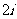
21.(本小题满分12分)
数列{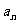 }满足:
}满足: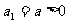 ,
,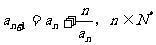 。
。
(1)证明:当 时,总有
时,总有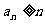 ;
;
(2)对任意一个给定的正整数 ,证明:存在
,证明:存在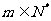 ,使当
,使当 时,总有
时,总有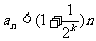 。
。
20.(本小题满分12分)
椭圆C1: 和双曲线C2:
和双曲线C2: 称为姊妹曲线,它们的离心率分别记为
称为姊妹曲线,它们的离心率分别记为 。
。
(1)求证: ;
;
(2)已知点M(2,1)是椭圆C1上一点,点P是椭圆C1与双曲线C2的渐近线在第一象限内的交点,过点P作椭圆C1的切线交双曲线C2于点Q,当△OPQ的面积等于1时,求双曲线C2的方程。
19.(本小题满分12分)
已知函数 。
。
(1)当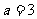 时,求函数
时,求函数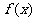 的极大值和极小值;
的极大值和极小值;
(2)若函数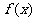 在(0,
在(0,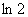 )上是单调递增函数,求实数
)上是单调递增函数,求实数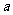 的取值范围。
的取值范围。
18.(本小题满分13分)
如下图,四棱锥P-ABCD中,底面ABCD为菱形,对角线AC与BD相交于点O,且PO⊥面ABCD。

(1)若M为棱PB的中点,求证:OM∥面PCD;
(2)若△BCD是边长为2的等边三角形,当侧棱PC长为多少时,二面角B-PC-D的大小为120°。
17.(本小题满分13分)
某人射击一次,击中目标的概率为0.8。
(1)若他连续射击5次,求其中恰好只有3次为连续击中目标的概率;
(2)规定:若此人射击一次,击中目标,则可继续进行一次射击,依此类推;若没有击中目标,则给他一次补射机会,但不管是否击中,均不能再射击。求他射击的平均次数。
16.(本小题满分13分)
已知函数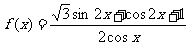 。
。
(1)求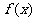 的定义域和值域;
的定义域和值域;
(2)若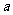 是△ABC的一个内角,且
是△ABC的一个内角,且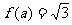 ,求
,求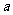 的值。
的值。
15.要排出某班一天中语文、数学、英语、物理、化学、生物6堂课的课程表,要求数学课排在上午(前4节)且比语文课后上,不同排法总数是_________。(以数字作答)
14.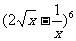 的展开式中,所有有理项的系数之和与所有无理项的系数之和的差为_________。
的展开式中,所有有理项的系数之和与所有无理项的系数之和的差为_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com