
20.(本小题满分12分)
如下图,已知椭圆的中心在坐标原点,焦点F1、F2在 轴上,长轴A1A2的长为4,左准线
轴上,长轴A1A2的长为4,左准线 与
与 轴的交点为M,
轴的交点为M,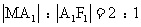 。
。

(1)求椭圆的方程;
(2)若直线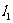 :
: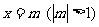 ,P为
,P为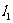 上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用
上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用 表示)。
表示)。
19.(本小题满分12分)
如下图,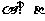 ,
, ,
,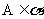 ,
, ,点A在直线
,点A在直线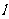 上的射影为
上的射影为 ,点B在
,点B在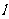 上的射影为
上的射影为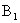 ,已知AB=2,AA1=1,BB1=
,已知AB=2,AA1=1,BB1=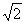 ,求:
,求:
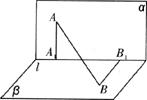
(1)直线AB分别与平面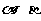 所成角的大小;
所成角的大小;
(2)二面角A1-AB-B1的大小。
18.(本小题满分13分)
已知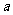 为实数,函数
为实数,函数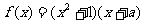 。
。
(1)若 ,求函数
,求函数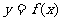 在
在 上的最大值和最小值;
上的最大值和最小值;
(2)若函数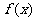 的图像上有与
的图像上有与 轴平行的切线,求
轴平行的切线,求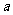 的取值范围。
的取值范围。
17.(本小题满分13分)
两个人射击,甲射击一次中靶概率是 ,乙射击一次中靶概率是
,乙射击一次中靶概率是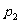 ,已知
,已知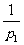 ,
,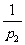 是方程
是方程 的根。
的根。
(1)求 ,
,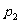 的值;
的值;
(2)两人各射击一次,中靶至少一次就算完成目的,则完成目的的概率是多少?
16.(本小题满分13分)
已知A、B、C是△ABC三内角,向量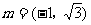 ,
,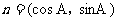 ,且
,且 。
。
(1)求角A;
(2)若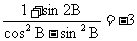 ,求
,求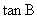 。
。
15.设直线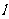 :
:
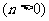 过点A(4,
过点A(4, ),若可行域
),若可行域 的外接圆直径为
的外接圆直径为 ,则实数
,则实数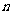 的值是__________。
的值是__________。
14.某校准备参加高中数学联赛,把10名选手名额分配到高三年级的8个班,每班至少一个名额,则分配方案有__________种。(用数字作答)
13.椭圆的焦点为F1、F2,过点F1作直线与椭圆相交,被椭圆截得的最短的线段MN长为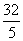 ,△MF2N的周长为20,则椭圆的离心率为__________。
,△MF2N的周长为20,则椭圆的离心率为__________。
12.若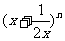 的展开式中前三项的系数成等差数,则展开式中
的展开式中前三项的系数成等差数,则展开式中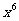 项的系数为__________。
项的系数为__________。
11.函数 的值域是__________。
的值域是__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com