
21.(本题满分12分)
已知点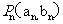 都在直线
都在直线 :y=2x+2上,P1为直线
:y=2x+2上,P1为直线 与x轴的交点,数列
与x轴的交点,数列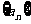 成等差数列,公差为1.(n∈N+)
成等差数列,公差为1.(n∈N+)
(1)求数列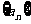 ,
,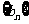 的通项公式;
的通项公式;
(2)若f(n)= 问是否存在k
问是否存在k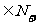 ,使得f(k+2011)=2f(k)-2成立;若存在,求出k的值,若不存在,说明理由.
,使得f(k+2011)=2f(k)-2成立;若存在,求出k的值,若不存在,说明理由.
(3)求证: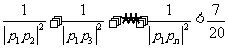 (n≥2,n∈N+)
(n≥2,n∈N+)
请考生在第22,23两题中任选一题做答,写出必要解答过程,如果多做,则按所做的第一题计分
20.(本题满分12分)
设椭圆E: 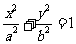 (a,b>0)过M(2,
(a,b>0)过M(2,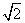 ) ,N(
) ,N(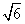 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且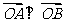 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在,说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在,说明理由。
19.(本题满分12分)
设函数 ,其中常数a>1.
,其中常数a>1.
(1)讨论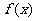 的单调性;
的单调性;
(2)若方程 在
在 时有唯一解,求实数
时有唯一解,求实数 的取值范围。
的取值范围。
18.(本题满分12分)
已知 是等比数列
是等比数列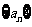 的前
的前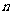 项和,
项和,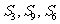 成等差数列,求证:
成等差数列,求证: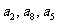 成等差数列.
成等差数列.
17.(本题满分12分)
某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间(以下简称购票用时,单位为min),表和图是这次调查统计分析所得到得频率分布表和频率分布直方图,解答下列问题.
|
分组 |
频数 |
频率 |
|
|
一组 |
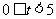 |
0 |
0 |
|
二组 |
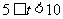 |
10 |
0.10 |
|
三组 |
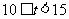 |
10 |
|
|
四组 |
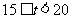 |
|
0.50 |
|
五组 |
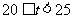 |
30 |
0.30 |
|
合计 |
100 |
1.00 |
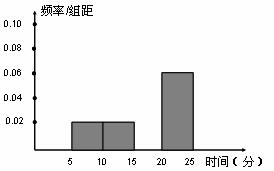
(1)写出这次抽样的样本容量是多少;
(2)在表中填写出缺失的数据,并补全频率分布直方图;
(3)旅客购票用时的平均数最可能落在哪一小组?
16.已知 是等差数列
是等差数列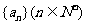 的前n项和,且
的前n项和,且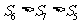 ,有下列四个命题:
,有下列四个命题:
⑴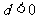 ;⑵
;⑵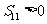 ;⑶
;⑶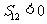 ;⑷ 数列
;⑷ 数列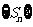 中的最大项为
中的最大项为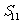 ,
,
其中正确的命题是 .(将所有正确的命题序号填在横线上).
15.某流感病毒是寄生在宿主的细胞内的,若该细胞开始时2个,记为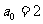 ,它们按以下规律进行分裂,1 小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1 个,……,记n小时后细胞的个数为
,它们按以下规律进行分裂,1 小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1 个,……,记n小时后细胞的个数为 ,则
,则 = ______ (用n表示)
= ______ (用n表示)
14.一列火车沿直线轨道前进,刹车后列车速度v(t)=24-0.8t,则列车刹车后前进 米
13.函数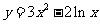 的单调增区间为
.
的单调增区间为
.
12.数列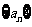 满足
满足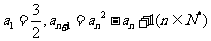 ,则
,则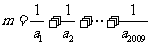 的整数部分是 ( )
的整数部分是 ( )
A.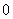 B.
B.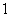 C.
C.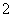 D.
D.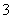
第Ⅱ卷(非选择题共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com