
3.
|
 ,且
,且 =
= 则 ( )
则 ( )
A.0≤ ≤
≤ B.
B. ≤
≤ ≤
≤

C. ≤
≤ ≤
≤ D.
D. ≤
≤ ≤
≤

2.“ ”是“函数
”是“函数 在区间
在区间 上为增函数”的 ( )
上为增函数”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.设集合 ,则满足
,则满足 的集合B的个数是 ( )
的集合B的个数是 ( )
A.1 B.3 C.4 D.8
21.(本题共3小题,其中第1小题4分,第2小题6分,第3小题8分,满分18分)
已知函数 。
。
(1)若函数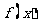 是
是 上的增函数,求实数
上的增函数,求实数 的取值范围;
的取值范围;
(2)当 时,若不等式
时,若不等式 在区间
在区间 (
( 为正常数)上恒成立,求实数
为正常数)上恒成立,求实数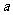 的取值范围;
的取值范围;
(3)对于函数 若存在区间
若存在区间 (
( ),使
),使 时,函数
时,函数 的值域也是
的值域也是 ,则称
,则称 是
是 上的闭函数。若函数
上的闭函数。若函数 (
( )是某区间上的闭函数,试探求
)是某区间上的闭函数,试探求 应满足的条件。
应满足的条件。
20.(本题共3小题,其中第1小题4分,第2小题6分,第3小题8分,满分18分)
对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “
是 “ 类数列”。
类数列”。
(1)若 ,
, ,
, ,数列
,数列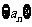 、
、 是否为“
是否为“ 类数列”?若是,指出它对应的实常数
类数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)若数列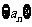 是“
是“ 类数列”,判断数列
类数列”,判断数列 是否是“M类数列”,并说明理由;
是否是“M类数列”,并说明理由;
(3)若数列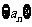 满足
满足 且
且 (
( ,
, 为非零常数),求数列
为非零常数),求数列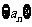 前
前 项的和;并判断
项的和;并判断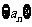 是否为“
是否为“ 类数列”,说明理由。
类数列”,说明理由。
19.(本题共2小题,其中第1小题6分,第2小题8分,满分14分)
如图,圆 与
与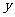 轴的正半轴交于点
轴的正半轴交于点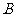 ,
, 是圆上的动点,
是圆上的动点, 点在
点在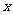 轴上的投影是
轴上的投影是 ,点
,点 满足
满足 。
。
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点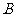 的直线
的直线 与
与 点的轨迹
点的轨迹 交于不同的两点
交于不同的两点 、
、 ,若
,若 ,求直线
,求直线 的方程。
的方程。

18.(本题共2小题,其中第1小题6分,第2小题6分,满分12分)
定义在 上的函数
上的函数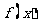 满足:对任意
满足:对任意 ,都有
,都有 成立,且当
成立,且当 时,
时, 。
。
(1)求 的值,并判断此函数在
的值,并判断此函数在 上的单调性;
上的单调性;
(2)当 时,解不等式
时,解不等式 。
。
17.(本题满分12分)
已知函数 ,求此函数在区间
,求此函数在区间 上的最大值和最小值,并求取得最值时
上的最大值和最小值,并求取得最值时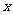 的值。
的值。
16.函数 的图像上存在不同的三点到原点的距离构成等比数列,则以下不可能成为公比的数是
( )
的图像上存在不同的三点到原点的距离构成等比数列,则以下不可能成为公比的数是
( )
A. B.
B. C.
C. D.
D.
15.已知两点 ,若直线上存在点
,若直线上存在点 ,使
,使 ,则称该直线为“
,则称该直线为“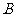 型直线”。现给出下列直线:
型直线”。现给出下列直线:
① ; ②
; ② ; ③
; ③ ; ④
; ④ 。
。
其中是“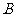 型直线”的是
( )
型直线”的是
( )
A.①② B.①③ C.②③ D.①④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com