
19.(本小题满分13分)已知数列{an},定义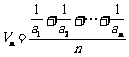 (n∈N+)是数列{an}的倒均数.
(n∈N+)是数列{an}的倒均数.
(1)若数列{an}的倒均数是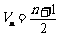 ,求数列{an}的通项公式;
,求数列{an}的通项公式;
(2)若等比数列{bn}的首项为–1,公比为q =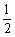 ,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
,其倒均数为Vn,问是否存在正整数m,使得当n≥m(n∈N+)时,Vn<–16恒成立?若存在,求m的最小值;若不存在,请说明理由.
18.(本小题满分12分)(1)解关于x的不等式:(x – 1)2>a(x – 2) + 1(a∈R).
(2)命题p: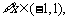 使不等式
使不等式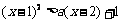 成立;
成立;
命题q: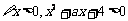 恒成立.
恒成立.
已知p或q为真,求实数a的取值范围.
17.(本小题满分12分)连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai,若存在正整数k,使a1 + a2 +…+ak = 6,则称k为你的幸运数字.
(1)求你的幸运数字为4的概率;
(2)若k = 1,则你的得分为6分;若k = 2,则你的得分为4分;若 k = 3,则你的得分为2分;若抛掷三次还没找到你的幸运数字则记0分.求得分 的分布列和数学期望.
的分布列和数学期望.
16.(本小题满分12分)已知△ABC的三个内角分别为A、B、C,向量m = (sinB, 1 – cosB)与向量n
= (2,0)夹角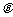 的余弦值为
的余弦值为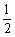 .
.
(1)求角B的大小;
(2)求sinA + sinC的取值范围.
15.由1,2,3,4,…, n为第一行,从第二行开始每行的每个数都等于其肩上两个数之和构成如图所示的三角形数表设f (i,j)( i,j =1,2,3,…, n且i + j≤n + 1, n∈N+)表示第i行的第j个数.
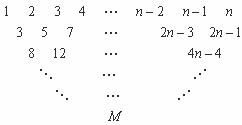
(1)当j≤n –3时,f (4, j)用j表示为 ;
(2)当n = 100时,M = .
14.已知函数f (x) = f (2 – x) + x + 3,则f ′(1) = .
13.已知函数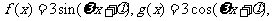 若对任意
若对任意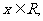 都有
都有
 则
则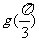 =________.
=________.
12.已知x,y,z均为实数,2x + y +z = 12,则x2 + y2 + z2 的最小值为 .
11.根据卫生部统计结果,全国范围内十一月上旬连续十天每天确诊甲流人数如下面的茎叶图所示,则这十天每天确诊甲流人数的平均值为 .

10.在腰长为2的等腰直角三角形ABC内任取一点,则该点到此三角形的直角顶点的距离小于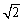 的概率为 .
的概率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com