19.(本题满分14分)某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩(均为整数)分成六段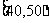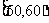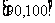，…后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：

(Ⅰ)求第四小组的频率，并补全这个频率分布直方图；

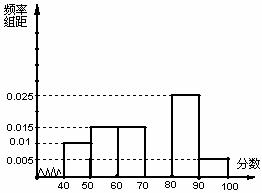
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分；

(Ⅲ)从成绩是70分以上(包括70分)的学生中选两人，求他们在同一分数段的概率.

18．(本题满分14分)设。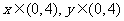

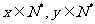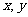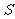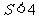(1)若，以作为矩形的边长，记矩形的面积为，求的概率；

(2)若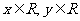，求这两数之差不大于2的概率。

17．(本题满分14分) 用0，1，2，3，4，5这六个数字

(1)可组成多少个不超过6位的不同的自然数？(数字可重复)

(2)可组成多少个无重复数字的五位数？

(3)可组成多少个无重复数字的五位奇数？

(4可组成多少个无重复数字的能被5整除的五位数？

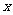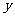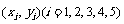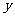16．(本题满分12分)假设关于某设备的使用年限和所支出的维修费用(万元),有如下的统计数据由资料知对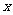呈线性相关,并且统计的五组数据得平均值分别为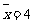,,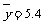若用五组数据得到的线性回归方程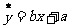去估计，使用8年的维修费用比使用7年的维修费用多1.1万元,

(1)求回归直线方程;

(2)估计使用年限为10年时，维修费用是多少?

15．(本题满分12分)某地现在居民住房的总面积为a m²,其中需要拆除的旧住房面积占了一半,当地有关部门决定在每年拆除一定数量旧住房的情况下,仍以10%的住房增长率建新住房。

(1)如果10年后该地的住房总面积正好比目前翻一番,那么每年应拆除的旧住房总面积x是多少?(可取1.1¹⁰≈2.6)

(2)过10年还未拆除的旧住房面积占当时住房面积的百分比是多少？(保留到小数点后第1位)

14．对于任意两个正整数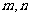，定义某种运算“*”如下：当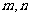都为正偶数或正奇数时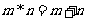，；当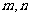一个为正偶数，另一个为正奇数时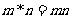，。则此定义下，集合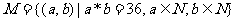元素的个数是。

13．某电视台连续播放5个广告，其中有3个不同的商业广告和2个不同的奥运宣传广告，要求最后播放的必须是奥运宣传广告，且2个奥运宣传广告不能连续播放，则不同的播放方式有种。

12．随机向边长为2的正方形ABCD中投一点P,则点P与A的距离不小于1且使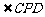为锐角的概率是__________________．

11．在△ABC中，三边的长为连续自然数，且最大角是钝角,这个三角形三边的长分别为___.

10．设a＞b＞0，试把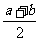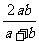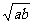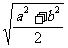，，，从大到小排列起来____________.