
5.命题p:“不等式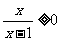 的解集为
的解集为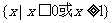 ”;命题q:“不等式
”;命题q:“不等式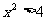 的解集为
的解集为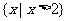 ”,则 ( )
”,则 ( )
A.p真q假 B.p假q真
C.命题“p且q”为真 D.命题“p或q”为假
4.已知数列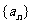 是公差为2的等差数列,且
是公差为2的等差数列,且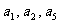 成等比数列,则a2为 ( ) A.-2 B.-3 C.2 D.3
成等比数列,则a2为 ( ) A.-2 B.-3 C.2 D.3
3.下列命题错误的是 ( )
A.命题“若p,则q”与命题“若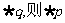 ”互为逆否命题
”互为逆否命题
B.命题“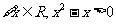 ”的否定是“
”的否定是“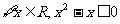 ”
”
C.“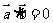 ”是“
”是“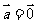 或
或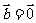 ”的必要不充分条件
”的必要不充分条件
D.“若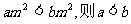 ”的逆命题为真
”的逆命题为真
2.已知函数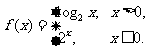 若
若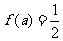 ,则
,则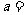 ( )
( )
A.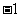 B.
B.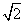 C.
C.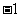 或
或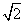 D.1或
D.1或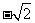
1.已知集合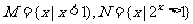 ,则
,则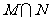 等于 ( )
等于 ( )
A.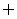 B.
B.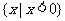 C.
C.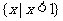 D.
D.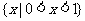
22.(本小题满分12分)已知函数 的最小值恰好是方程
的最小值恰好是方程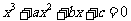 的三个解,其中
的三个解,其中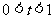 .
.
(I)求证: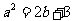
(II)设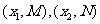 是函数
是函数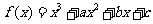 的两个极值点。
的两个极值点。
①若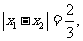 求函数
求函数 的解析式;②求
的解析式;②求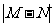 的取值范围。
的取值范围。
21.(本小题满分12分) 定义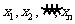 的“倒平均数”为
的“倒平均数”为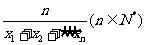 ,已知数列
,已知数列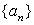 前
前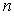 项的“倒平均数”为
项的“倒平均数”为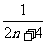 .
.
(I)记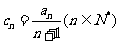 ,试比较
,试比较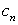 与
与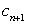 的大小;
的大小;
(II)是否存在实数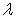 ,使得当
,使得当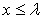 时,
时,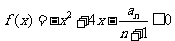 对任意
对任意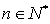 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数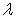 ;若不存在,说明理由.
;若不存在,说明理由.
20.(本小题满分12分)设数列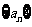 的前
的前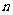 项和为
项和为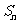 ,如果
,如果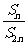 为常数,则称数列
为常数,则称数列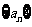 为“科比数列”.
为“科比数列”.
(Ⅰ)已知等差数列 的首项为1,公差不为零,若
的首项为1,公差不为零,若 为“科比数列”,求
为“科比数列”,求 的通项公式;
的通项公式;
(Ⅱ)设数列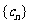 的各项都是正数,前
的各项都是正数,前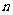 项和为
项和为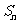 ,若
,若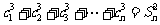 对任意
对任意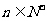 都成立,试推断数列
都成立,试推断数列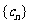 是否为“科比数列”?并说明理由.
是否为“科比数列”?并说明理由.
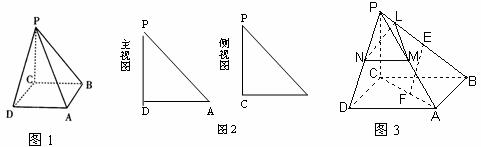
19.(本小题满分12分)如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
(Ⅰ)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(Ⅱ)图3中,L、E均为棱PB上的点,且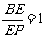 ,
,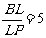 ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
18.(本小题满分12分)某创业投资公司拟投资开发某种新能源产品,估计能获得10万元-1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(Ⅰ)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;
(Ⅱ)现有两个奖励函数模型:(1)y=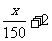 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com