
19.(本小题满分14分)
已知数列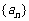 的前
的前 项和
项和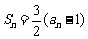 ,
, .
.
(1)求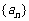 的通项公式;
的通项公式;
(2)设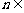 N+,集合
N+,集合 ,
,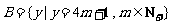 .现在集合
.现在集合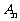 中随机取一个元素
中随机取一个元素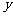 ,记
,记 的概率为
的概率为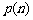 ,求
,求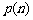 的表达式.
的表达式.
18.(本小题满分14分)
如图,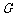 是△
是△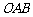 的重心,
的重心,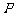 、
、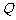 分别是边
分别是边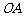 、
、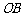 上的动点,且
上的动点,且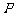 、
、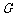 、
、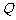 三点共线.
三点共线.
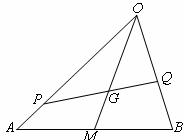
(1)设 ,将
,将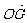 用
用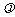 、
、 、
、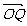 表示;
表示;
(2)设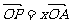 ,
,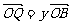 ,证明:
,证明: 是定值;
是定值;
(3)记△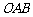 与△
与△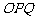 的面积分别为
的面积分别为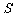 、
、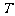 .求
.求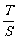 的取值范围.
的取值范围.
17.(本小题满分14分)
已知函数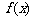 满足
满足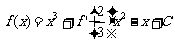 (其中
(其中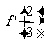 为
为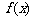 在点
在点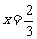 处的导数,
处的导数,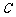 为常数).
为常数).
(1)求函数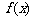 的单调区间;
的单调区间;
(2)若方程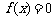 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数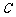 ;
;
(3)在(2)的条件下,若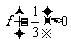 ,求函数
,求函数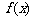 的图象与
的图象与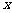 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.
16.(本小题满分12分)
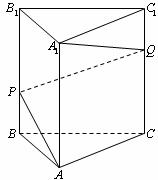
如下图,正三棱柱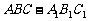 中,
中,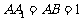 ,
,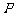 、
、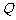 分别是侧棱
分别是侧棱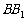 、
、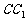 上的点,且使得折线
上的点,且使得折线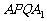 的长
的长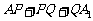 最短.
最短.
(1)证明:平面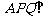 平面
平面 ;
;
(2)求直线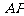 与平面
与平面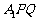 所成角的余弦值.
所成角的余弦值.
15.(本小题满分12分)
设有同频率的两个正弦电流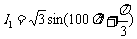 ,
, ,把它们合成后,得到电流
,把它们合成后,得到电流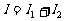 .
.
(1)求电流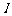 的最小正周期
的最小正周期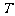 和频率
和频率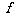 ;
;
(2)设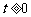 ,求电流
,求电流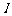 的最大值和最小值,并指出
的最大值和最小值,并指出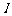 第一次达到最大值和最小值时的
第一次达到最大值和最小值时的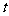 值.
值.
14.给出下列四个命题:
①设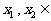 R,则
R,则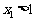 且
且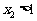 的充要条件是
的充要条件是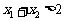 且
且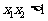 ;
;
②任意的锐角三角形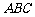 中,有
中,有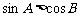 成立;
成立;
③平面上 个圆最多将平面分成
个圆最多将平面分成 个部分;
个部分;
④空间中直角在一个平面上的正投影可以是钝角.
其中真命题的序号是 (要求写出所有真命题的序号).
13.如图,有一轴截面为正三角形的圆锥形容器,内部盛水的高度为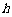 ,放入一球后,水面恰好与球相切,则球的半径为 (用
,放入一球后,水面恰好与球相切,则球的半径为 (用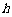 表示).
表示).

12.若偶函数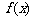 在
在 内单调递减,则不等式
内单调递减,则不等式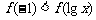 的解集是 .
的解集是 .
11.据研究,甲、乙两个磁盘受到病毒感染,感染的量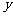 (单位:比特数)与时间
(单位:比特数)与时间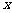 (单位:秒)的函数关系式分别是
(单位:秒)的函数关系式分别是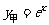 和
和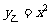 .显然,当
.显然,当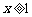 时,甲磁盘受到的病毒感染增长率比乙磁盘受到的病毒感染增长率大.试根据上述事实提炼一个不等式是 .
时,甲磁盘受到的病毒感染增长率比乙磁盘受到的病毒感染增长率大.试根据上述事实提炼一个不等式是 .
10.若△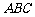 的三个内角满足
的三个内角满足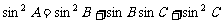 ,则
,则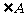 等于 .
等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com