
17.(本小题满分12分)
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,且PB//平面AMC。
(1)试确定点M的位置;
(2)若点N是PB的中点,求证:MN⊥平面PAC。

16.(本小题满分12分)
已知 ,其中向量
,其中向量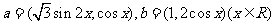
(1)求 的最小正周期;
的最小正周期;
(2)在△ABC中,角A、B、C的对边分别为a、b、c, ,求边长
,求边长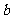 的值。
的值。
15.定义在R上的偶函数 满足条件:①对任意正实数
满足条件:①对任意正实数 ,且
,且 ,都有
,都有
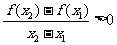 ;②
;② ,则:
,则:
(1)不等式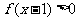 的解集是_____________________;
的解集是_____________________;
(2)若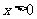 时,
时, ,则
,则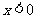 时,
时,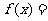 ___________。
___________。
14.若直线 平面圆
平面圆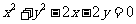 ,则:
,则:
(1) 满足的条件是______________;(2)
满足的条件是______________;(2) 的最小值是___________。
的最小值是___________。
13.若一个底面为正三角形、侧棱与底面 垂直的棱柱的三视图如下图所示,则这个棱柱的体积为_________。
垂直的棱柱的三视图如下图所示,则这个棱柱的体积为_________。

12.已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,
△ABF2是正三角形,则这个椭圆的离心率是__________。
11.过点(-1,1)作直线与圆 相交,则所得弦的长度最短时,直线的斜率是____
_。
相交,则所得弦的长度最短时,直线的斜率是____
_。
10.已知命题: ,若命题
,若命题 是假命题,则实数
是假命题,则实数 的取值范围是__________。
的取值范围是__________。
9.若 则
则 __________
__________
8.若函数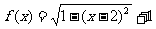 ,则对任
,则对任 意的
意的 ,有 ( )
,有 ( )
A. B.
B.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com