
4.设 为平面,给出条件:
为平面,给出条件:
(1)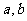 为异面直线,
为异面直线, //
// ,
,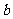 //
//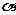
(2)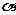 内不共线的三点到
内不共线的三点到 的距离相等
的距离相等
(3)

(4) //
//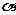 ,
, //
//
则其中能使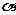 //
// 成立的条件的个数是几个( )
成立的条件的个数是几个( )
A.3 B.2 C.1 D.0
3.函数 的单调增区间是( )
的单调增区间是( )
A.( B.(
B.( C.
C. D.(3,
D.(3, )
)
2.已知函数 的图象经过点(0,-2),那么函数
的图象经过点(0,-2),那么函数 的反函数图象一定经过点( )
的反函数图象一定经过点( )
A.(0,-1) B.(-1,0) C.(0,1) D.(1,0)
1.下列命题中正确的是( )
A.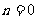 时,幂函数
时,幂函数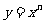 的图象是一条直线
的图象是一条直线
B.幂函数的图象一定过点(0,0)和点(1,1)
C.若幂函数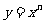 是奇函数,则其一定是单调函数
是奇函数,则其一定是单调函数
D.幂函数的图象不可能经过第四象限
20.(本小题满分14分)
设函数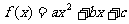 (
( ,
, ,
, 为实数,且
为实数,且 ≠0),
≠0),
(Ⅰ)若 ,曲线
,曲线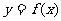 通过点
通过点 ,且在点
,且在点 处的切线垂直于
处的切线垂直于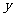 轴,求
轴,求 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围;
的取值范围;
(Ⅲ)设 ,
, ,
, ,且
,且 为偶函数,证明
为偶函数,证明 .
.
19.(本小题满分14分)
已知椭圆C的中心在原点,一个焦点F(-2,0),且长轴长与短轴长的比是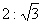 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
18.(本小题满分13分)
设数列 的前
的前 项和为
项和为 ,已知
,已知 ,
,
(Ⅰ)求证:数列 为等差数列,并写出
为等差数列,并写出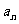 关于
关于 的表达式;
的表达式;
(Ⅱ)若数列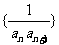 前
前 项和为
项和为 ,问满足
,问满足 的最小正整数
的最小正整数 是多少?
是多少?
17.(本小题满分13分)
已知函数 在
在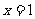 处有极值
处有极值 .
.
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)判断函数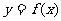 的单调性并求出单调区间.
的单调性并求出单调区间.
16.(本小题满分14分)
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,E是SD的中点.

(Ⅰ)求证:SB∥平面EAC;
(Ⅱ)求证:AC⊥BE.
15.(本小题满分12分)
已知向量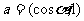 ,
, ,
, ,且
,且 ⊥
⊥ .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com