21．(本题满分l 2分)

　　　 如图，已知圆经过椭圆的右焦点F及上顶点B。过椭圆外一点(m，0)(m>a)倾斜角为的直线l交椭圆于C、D两点．

　 (1)求椭圆的方程；

　 (2)若右焦点F在以线段CD为直径的圆E的内部，求m的取值范围．

20．(本题满分1 2分)

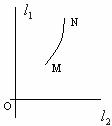
　　　 如图，，是通过某市开发区中心O的两条南北和东西走向的道路，连接M、N两地的铁路是一段抛物线弧，它所在的抛物线关于直线L₁对称。M到L₁、L₂的距离分别是2 km、4km，N到L₁、L₂的距离分别是3 km、9 km．

　 (1)建立适当的坐标系，求抛物线弧MN的方程；

　 (Ⅱ)该市拟在点O的正北方向建设一座工厂，考虑到环境问题，要求厂址到点O的距离大于5km而不超过8km，并且铁路上任意一点到工厂的距离不能小于km．求 此厂离点O的最近距离．(注：工厂视为一个点)

19．(本题满分1 2分)

　　　 已知数列{a_n}是首项a₁=1的等比数列，且a_n>0，{b_n}是首项为l的等差数列，又a₅+b₃=21，a₃+b₅=13．

　 (1)求数列{a_n}和{b_n}的通项公式

　 (2)求数列的前n项和S_n．

18．(本题满分12分)

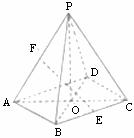
　　　 如图，在四棱锥P-ABCD中，底面是边长为 2的菱形，∠BAD=60°，对角线AC与BD相交于点O，PO⊥底ABCD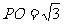，,E、F分别是BC、AP的中点．

　 (1)求证：EF∥平面PCD；

　 (2)求二面角A-BP-D的余弦值．

17．(本题满分1 2分)

　　　 如图，以Ox为始边作角a与β()，它们终边分别α与β()单位圆相交于点P、Q，已知点P的坐标为(，)

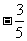　 (1)求的值；

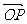　 (2)若·，求。

16．给出下列四个命题：

　　　 ①函数在区间上存在零点

②若=0，则函数在取得极值；

③≥-1，则函数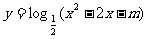的值域为R；

④“”是“函数在定义域上是奇函数”的充分不必要条件。

其中真命题是　　　　　　 (把你认为正确的命题序号都填在横线上)

15．已知A船在灯塔C北偏东80。处，且A到C的距离为2km，B船在灯塔C北偏西

40°，A、B两船的距离为3 km，则B到C的距离为　　　 km．

14．若中心在坐标原点，对称轴为坐标轴的椭圆经过两点(4，0)和(0，2)，则该椭圆的离心率等于　　　　　　　 。

13．已知等比数列{a_n}中，a₁=3，a₄=81，若数列{b_n}满足b_n=log₃ a_n，则数列 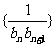的前n项和Sn=　　　　　　　　 。

12．已知y=f(x)是定义在R上的增函数，函数y=f(x-1)的图象关于点(1，0)对称．若对任意的x，y∈R，不等式f(x²-6x+21)+f(y²-8y)<0恒成立，则当x>3时，x²+y²的取值范围是　　　　　　　　　　　　　　 (　　 )

　　　 A．(3，7)　　 　　　 B．(9，25)　　 　　 C．(13，49)　　 　 D．(9，49)

第Ⅱ卷　 (非选择题共90分)