5．设等差数列{a_n}的前n项和为S_n，若S₃=9，S₆=36，则a₇+a₈+a₉等于

A．63　　 　　　　　　　　　 B．45 　　　　　　　　　　　 C．36　　 　　　　　　　　　 D．27

4．函数y=log_ax和y=(1-a)x+a的图象只可能是

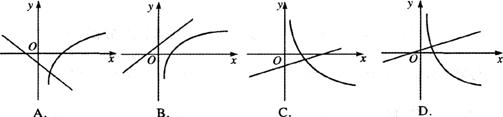
3．命题：“若x²<1，则-1<x<1”的逆否命题是

A．若x≥1，或x≤-1，则x²≥1　　 　　　　　　　　　 B．若-1<x<1，则x²<1

C．若x>1，或x<-1，则x²>1　　 　　　　　　　　　 D．若x²≥1，则x≥1，或x≤-1

2．sin315⁰-cos135⁰+2sin570⁰的值是

A．1　　 　　　　　　　　　　 B．-1 　　　　　　　　　　　 C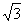．　　 　 　　　　　　　 D．-

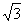
1．已知集合M={0，1，2}，N={x| x=2a，a∈M}，则集合M∩N为

A．{0}　　 　　　　　　　　 B．{0，1}　 　 　　　　　　 C．{1，2}　　 　　　　　　 D．{0，2}

22．(本小题满分14分)

设函数f(x)=(1+x)²-2ln(1+x)．

(I)若在定义域内存在x₀，使得不等式f(x₀)-m≤0能成立，求实数m的取值范围；

(II)若函数g(x)=f(x)-x²-x-a在区间[0，2]上恰有两个不同的零点，求实数a的取值范围．

21．(本小题满分12分)

已知数列{a_n}的前n项和．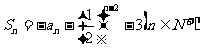

(I)令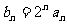．求证数列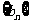是等差数列，并求b_n

(Ⅱ)数列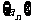中是否存在最大项?如果存在，求出最大项；如果不存在，说明理由．

20．(本小题满分12分)

某工厂生产某种产品，每件产品的成本为300元，并且每件产品的加工费为t元(其中t为常数，且20≤t≤50)，设该工厂每件产品的售价为x元(350≤x≤410)，根据市场调查，日销售量与e^x(e为自然对数的底数)成反比例，当每件产品的售价为400元时。日销售量为100件．

(I)求该工厂的日利润y(元)与每件产品的售价x元的函数关系式；

(Ⅱ)当每件产品的售价为多少元时，该工厂的日利润y最大，并求y的最大值．

19．(本小题满分12分)

已知函数f(x)=sinx+cosx，g(x)=cosx-sinx

(I)求函数F(x)=f(x)g(x)+f²(x)的最大值和取得最大值时x的值

(Ⅱ)若f(x)=2g(x)，求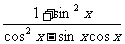的值．

18．(本小题满分12分)

已知命题p：方程x²-(2m-2)x+m²-2m=0在[1，3]上有解；命题q：函数y=ln(x²+mx+1)的值域是R．如果命题“p或q”为假命题，求m的取值范围．