20．(本小题满分13分)

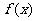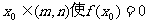　　　　 定理：若函数在闭区间[m，n]上是连续的单调函数，且，则存在唯一一个。已知

　 (1)若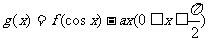是减函数，求a的取值范围。

　 (2)是否存在同时成立，若存在，指出c、d之间的等式关系，若不存在，请说明理由。

19．(本小题满分12分)

　　　　 已知：经过点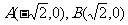的动圆与y轴交于M、N两点，C(-1，0)，D(1，0)是x轴上两点，直线MC与ND相交于P。

　 (1)求点P的轨迹E的方程；

　 (2)直线GH交轨迹E于G、H两点，并且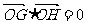(O是坐标原点)，求点O到直线GH的距离。

18．(本小题满分12分)

　　　　 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，过D与PB垂直的平面分别交PB、PC于F、E。

　 (1)求证：DE⊥PC；

　 (2)当PA//平面EDB时，求二面角E-BD-C的正切值。

17．(本小题满分12分)

　　　　 已知函数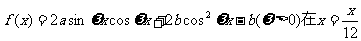时取最大值2。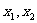是集合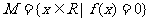中的任意两个元素，的最小值为

　 (1)求a、b的值；

　 (2)若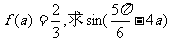的值。

16．(本小题满分12分)

　　　　 袋中有大小相同的5个球，其中黑球3个，白球2个，甲乙二人分别从中各取一个，甲先取(不放回)乙后取。

　 (1)分别求甲乙取到黑球的概率；

　 (2)求两人共取到黑球的个数的数学期望。

15．对于函数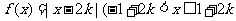，其中k可以取所有整数)下列三种结论中正确的有　　　　　 (只填你认为正确结论的序号)

　　 ①使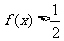的x的取值集合为；

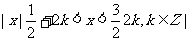②函数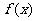的图像是中心对称图形，点是其对称中心；

③函数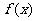的图像按向量平移得到一个奇函数的图像。

14．北京大学今年实施校长实名推荐制，某中学获得推荐4名学生的资格，校长要从7名优秀学生中推荐4名，7名学生中有2人有体育特长，另有2人有艺术特长，其余3人有其他特长，那么至少含有一名有体育特长和一名有艺术特长的学生的推荐方案有　　　

　　 种(用数字作答)。

13．设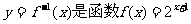的反函数，若，则a+b的最小值为　 　　　　　　　　　　。

12．过抛物线焦点的直线交抛物线于A、B两点，过B点作抛物线的准线的垂线，垂足为C，已知点A(4，4)，则直线AC的方程为　　　　　　 。

11．已知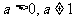，若函数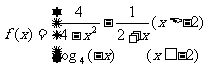在点x=-2处连续，则a=

　　 　　　　　　　　。