
23.(选修4-4:坐标系与参数方程)
已知直线l的参数方程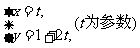 和圆C的极坐标方程
和圆C的极坐标方程 .
.
(1)将直线l的参数方程化为普通方程,将圆C的极坐标方程化为直角坐标方程;
(2)判断直线l和圆C的位置关系.
22.(选修4-1:几何证明选讲)
如图,AD是△ABC的内角平分线,延长AD交△ABC的外接圆O于点E,过C、D、E三点的圆O1交AC的延长线于点F,连结EF、DF。
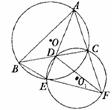
(1)求证:△AEF∽△FED;
(2)若AD=6,DE=3,求EF的长.
21.已知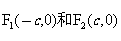 分别是椭圆
分别是椭圆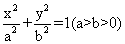 的左、右焦点,B是其上顶点,点N的坐标是
的左、右焦点,B是其上顶点,点N的坐标是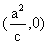 ,满足
,满足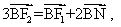
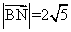 .
.
(1)求此椭圆的方程;
(2)若M是坐标平面内一动点,G是三角形MF1F2的重心,且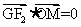 ,其中O是坐标原点,求动点M的轨迹C的方程;
,其中O是坐标原点,求动点M的轨迹C的方程;
(3)点P是此椭圆上一点,但非短轴端点,并且过P可作(2)中所求得轨迹C的两条不同的切线,Q、R是两个切点,求 的最小值.
的最小值.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,按所做的第一题记分。
20.设 、
、
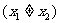 是函数
是函数 的两个极值点。
的两个极值点。
(1)若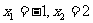 ,求函数
,求函数 的解析式;
的解析式;
(2)若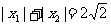 ,求
,求 的最大值。
的最大值。
(3)若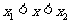 ,且
,且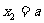 ,
, ,求证:
,求证: 。
。
19.某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可通过。已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都为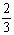 ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算其数学期望;
(2)试用统计知识分析比较两考生的实验操作能力。
18.如图,三棱柱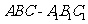 的底面是边长为a的正三角形,侧面
的底面是边长为a的正三角形,侧面 是菱形且垂直于底面,∠
是菱形且垂直于底面,∠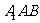 =60°,
=60°,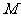 是
是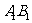 的中点.
的中点.

(1)求证: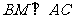 ;
;
(2)求二面角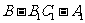 的正切值。
的正切值。
17.已知向量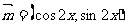 ,
,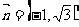 ,
, .
.
(1)当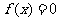 时,求角x的取值集合;
时,求角x的取值集合;
(2)求函数 的单调区间,并求出使得
的单调区间,并求出使得 取得最大值的对应向量
取得最大值的对应向量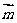 .
.
16.已知函数 ,正实数
,正实数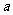 、
、 、
、 成公差为正数的等差数列,且满足
成公差为正数的等差数列,且满足 ,若实数
,若实数 是方程
是方程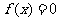 的一个解,那么下列四个判断:
的一个解,那么下列四个判断:
①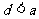 ;②
;② ;③
;③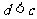 ;④
;④ ,其中有可能成立的判断的序号是 (请把你认为正确的都填上).
,其中有可能成立的判断的序号是 (请把你认为正确的都填上).
15.已知 、
、 是双曲线
是双曲线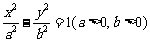 的两个焦点,M为双曲线上的点,若
的两个焦点,M为双曲线上的点,若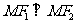 ,
,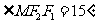 ,则双曲线的离心率为
;
,则双曲线的离心率为
;
14.若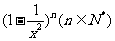 的展开式中
的展开式中 的系数为
的系数为 ,则
,则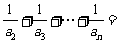 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com