
2.(矩阵与变换选做题)
求直线 在矩阵
在矩阵 作用下变换得到的直线的方程。
作用下变换得到的直线的方程。
1.(集合证明选讲选做题)
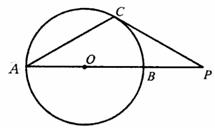
如图AB是·O的直径,点P在AB的延长线上,PC与·O相切于点C,PC=AC=1,求·O的半径。
20.(本题满分16分,第1小题4分,第2小题6分,第3小题6分)
设函数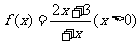 ,数列
,数列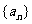 满足
满足 ,
,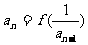 (
( ∈N*,且
∈N*,且 ≥2)。
≥2)。
(1)求数列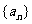 的通项公式;
的通项公式;
(2)设 ,若
,若 ≥
≥ 对
对 ∈N*恒成立,求实数
∈N*恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在以 为首项,公比为
为首项,公比为 (
(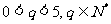 )的数列
)的数列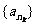 ,
, ,使得数列
,使得数列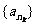 中的每一项都是数列
中的每一项都是数列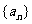 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由。
的通项公式;若不存在,说明理由。
附 加 题
解答题(本大题满分40分,1-4题为选做题,每题10分,考生只需选做其中2题,多选做的以前两题计分,5-6题为必做题,每题10分)
19.(本题满分16分,第1小题4分,第2小题4分,第3小题8分)
已知函数 在点(1,
在点(1,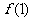 )处的切线方程为
)处的切线方程为 .
.
(1)求函数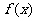 的解析式;
的解析式;
(2)若对于区间 上任意两个自变量的值
上任意两个自变量的值 ,
,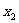 ,都有
,都有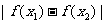 ≤
≤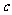 ,求实数
,求实数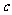 的最小值。
的最小值。
(3)若果点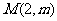 (
(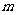 ≠2)可作曲线
≠2)可作曲线 的三条切线,求实数
的三条切线,求实数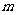 的取值范围。
的取值范围。
18.(本题满分16分,第1小题6分,第2小题10分)
已知椭圆 的楼离心率为
的楼离心率为 ,
,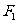 、
、 分别为椭圆C的左、右焦点,若椭圆C的焦距为2.
分别为椭圆C的左、右焦点,若椭圆C的焦距为2.
(1)求椭圆C的方程;
(2)设M为椭圆上任意一点,以M为圆心, 为半径作圆M,当圆M于椭圆的右准线
为半径作圆M,当圆M于椭圆的右准线 有公共点,求△
有公共点,求△ 面积的最大值。
面积的最大值。
17.(本题满分14分)
如图,矩形ABCD是机器人踢球的场地,AB=170cm,AD=80cm,机器人先从AD中点E进入场地到点F处,EF=40cm,EF⊥AD。场地内有一小球从B点向A点运动,机器人从F点出发去截小球。现机器人和小球同时出发,它们均作直线运动,并且小球运动的速度是机器人行走速度的2倍。若忽略机器人圆底旋转所需的时间,则机器人最快可在何处截住小球?

16.(本题满分14分,第1小题6分,第2小题8分)
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE。

(1)求证:AE⊥BC;
(2)如果点N为线段AB的中点,求证:MN∥平面ADE.
15.(本题满分14分,第1小题5分,第2小题9分)
已知 ,
, ,
,
(1)若 ∥
∥ ,求
,求 的值;
的值;
(2)若 ·
·
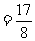 ,求
,求 的值。
的值。
14.设M是由满足下列性质的函数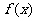 构成的集合:
构成的集合:
在定义域内存在 ,使得
,使得 =
=
 成立。已知下列函数:
成立。已知下列函数:
① ; ②
; ② ; ③
; ③ ;④
;④ ,
,
其中属于集合M的函数是 。(写出所有满足要求的函数的序号)。
13.五位同学围成一圈依次循环报数,规定:第一位同学首次报出的数为2,第二位同学首次报出的数为3,之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字,则第2010个被报出的数为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com