
22.(本小题满分12分)
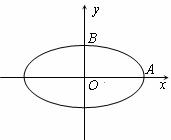
如图,已知点A、B是椭圆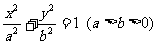 的两个顶点,若点C(t,t)(t>0)在椭圆上,且满足
的两个顶点,若点C(t,t)(t>0)在椭圆上,且满足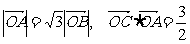 .(其中O为坐标原点)
.(其中O为坐标原点)
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l与椭圆交于两点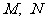 ,当
,当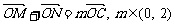 时,求
时,求 面积的最大值。
面积的最大值。
21.(本小题满分12分)
定义在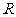 上的函数
上的函数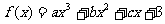 同时满足以下条件:
同时满足以下条件:
① 在
在 上是增函数,在
上是增函数,在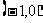 上是减函数;②
上是减函数;② 的导函数是偶函数;
的导函数是偶函数;
③ 在
在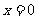 处的切线与第一、三象限的角平分线垂直.
处的切线与第一、三象限的角平分线垂直.
(Ⅰ)求函数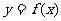 的解析式;
的解析式;
(Ⅱ)设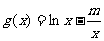 ,若存在
,若存在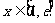 ,使
,使 ,求实数
,求实数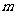 的取值范围.
的取值范围.
20.(本小题满分12分)
已知数列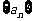 的前
的前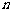 项和为
项和为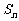 ,
,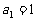 ,且
,且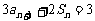 (
(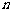 为正整数)
为正整数)
(Ⅰ)求出数列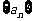 的通项公式;
的通项公式;
(Ⅱ)若对任意正整数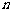 ,
,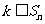 恒成立,求实数
恒成立,求实数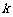 的最大值.
的最大值.
19.(本小题满分12分)
甲、乙两种鱼的身体吸收汞,当汞的含量超过体重的1.00ppm(即百万分之一)时,就会对人体产生危害。质检部门对市场中出售的一批鱼进行检测,在分别抽取的10条鱼的样本中,测得汞含量与鱼体重的百分比如下:
甲种鱼1.31 1.55 1.42 1.35 1.27 1.44 1.28 1.37 1.36 1.14
乙种鱼1.01 1.35 0.95 1.16 1.24 1.08 1.17 1.03 0.60 1.11
(Ⅰ)用前两位数做茎,画出样本数据的茎叶图,并回答下面两个问题:
(ⅰ)写出甲、乙两种鱼关于汞分布的一个统计结论.
(ⅱ)经过调查,市场上出售汞超标的鱼的原因是这些鱼在出售前没有经过检验,可否得出每批这两种鱼的平均汞含量都超过1.00ppm?
(Ⅱ)如果在样本中选择甲、乙两种鱼各一条做一道菜,(在烹饪过程中汞含量不会发生改变)
(ⅰ)如果20条鱼中的每条鱼的重量都相同,那么这道菜对人体产生危害的概率是多少?
(ⅱ)根据算出的结论,你对政府监管部门有什么建议?(提出一条建议即可)
18.(本小题满分12分)
下图是一个直三棱柱(以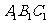 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为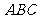 .
.
已知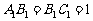 ,
, 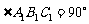 ,
,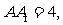
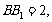
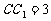 .
.
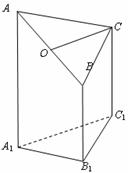
(Ⅰ)设点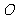 是
是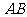 的中点,证明:
的中点,证明: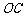 ∥平面
∥平面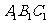 ;
;
(Ⅱ)求二面角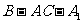 的大小.
的大小.
17.(本小题满分10分)
已知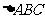 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为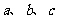 ,向量
,向量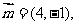
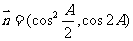 ,且
,且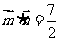 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若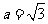 ,bc=3,试判断
,bc=3,试判断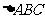 形状.
形状.
16.已知函数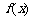 的定义域为[-2,+∞),部分对应值如下表,
的定义域为[-2,+∞),部分对应值如下表,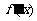 为
为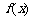 的导函数,函数
的导函数,函数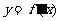 的图象如下图所示,若两正数a,b满足
的图象如下图所示,若两正数a,b满足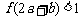 ,则
,则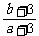 的取值范围是 .
的取值范围是 .


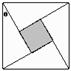
15.如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角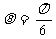
 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是___
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是___
14.在三棱锥P-ABC中,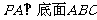 ,
, ,
,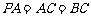 ,则两直线PC与AB所成角的大小是 .
,则两直线PC与AB所成角的大小是 .
13.观察下列式子: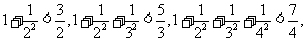 ……,则可以猜想:
……,则可以猜想:
当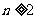 时,有
.
时,有
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com