
2.函数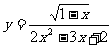 的定义域是
的定义域是
A. B.
B.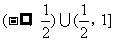
C. D.
D.
1.已知集合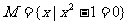 ,则有
,则有
A.
 B.
B. C.
C. D.
D.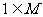
4.(本题满分12分)
试比较 与
与 的大小。
的大小。
当 时,有
时,有

 填>、=或<
填>、=或<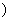
当 时,有
时,有

 填>、=或<
填>、=或<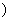
当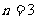 时,有
时,有

 填>、=或<
填>、=或<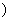
当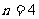 时,有
时,有

 填>、=或<
填>、=或<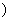
猜想一个一般性结论,并加以证明。
3.(本题满分12分)
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF-90°,BE∥CF,CE⊥EF,AD= ,EF=2.
,EF=2.
(1)求异面直线AD与EF所成的角;
(2)当AB的长为何值时,二面角A-EF-C的大小为45°?

2.(本题满分8分)
已知动抛物线的准线为 轴,且经过点(0,2),求抛物线的顶点轨迹方程。
轴,且经过点(0,2),求抛物线的顶点轨迹方程。
20.(本题满分16分)
由部分自然数构成如图的数表,用 表示第
表示第 行第
行第 个数(
个数( ),使
),使 ,每行中的其余各数分别等于其“肩膀”上的两个数的之和。设第
,每行中的其余各数分别等于其“肩膀”上的两个数的之和。设第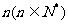 行中各数之和为
行中各数之和为 。
。

(1)求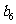 ;
;
(2)用 表示
表示 ;
;
(3)试问:数列 中是否存在不同的三项
中是否存在不同的三项 ,
, ,
, (
( )恰好成等差数列?若存在,求出
)恰好成等差数列?若存在,求出 ,
,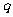 ,
, 的关系;若不存在,请说明理由。
的关系;若不存在,请说明理由。
数学(理科)加试题
写出 的二项展开式(
的二项展开式( 为虚数单位),并计算
为虚数单位),并计算 的值。
的值。
19.(本题满分16分)
已知函数 为奇函数,且
为奇函数,且 在
在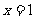 处取得极大值2.
处取得极大值2.
(1)求函数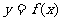 的解析式;
的解析式;
(2)记 ,求函数
,求函数 的单调区间;
的单调区间;
(3)在(2)的条件下,当 时,若函数
时,若函数 的图像的直线
的图像的直线 的下方,求
的下方,求 的取值范围。
的取值范围。
18.(本题满分16分)
设椭圆 的左,右两个焦点分别为
的左,右两个焦点分别为 ,
, ,短轴的上端点为B,短轴上的两个三等分点为P,Q,且
,短轴的上端点为B,短轴上的两个三等分点为P,Q,且 为正方形。
为正方形。
(1)求椭圆的离心率;
(2)若过点B作此正方形的外接圆的切线在 轴上的一个截距为
轴上的一个截距为 ,求此椭圆方程。
,求此椭圆方程。

17.(本题满分14分)
设函数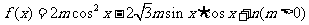 的定义域为
的定义域为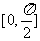 ,值域为
,值域为 。
。
(1)求 ,
, 的值;
的值;
(2)若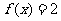 ,求
,求 的值。
的值。
16.(本题满分14分)
已知正六棱柱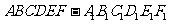 的所有棱长均为2,G为AF的中点。
的所有棱长均为2,G为AF的中点。

(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)求四面体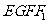 的体积。
的体积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com