5. 4名学生从3个不同的楼梯下楼的方法数.

4.将3封信投入4个不同的邮筒的投法共有多少种?

3.集合A=｛a,b,c,d,e｝,集合B=｛1,2,3｝,问A到B的不同映射f共有多少个?B到A的映射g共有多少个?

2.用数字1,2,3可写出多少个小于1000的正整数? (各位上的数字允许重复)

1.用1,2,3,4,5可组成多少个三位数?(各位上的数字允许重复)

(2)奇约数中步不含有2的因数,因此75600的每个奇约数都可以写成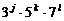的形式,同上奇约数的个数为4×3×2=24个.

于是,要确定75600的一个约数,可分四步完成,即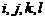分别在各自的范围内任取一个值,这样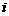有5种取法,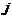有4种取法,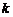有3种取法,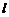有2种取法,根据分步计数原理得约数的个数为5×4×3×2=120个.

(1) 75600的每个约数都可以写成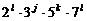的形式,其中,,,

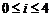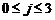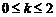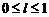
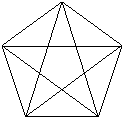第一类:其中有两条边是原五边形的边,这样的三角形共有5个

第二类:其中有且只有一条边是原五边形的边,这样的三角形共有5×4=20个

第三类:没有一条边是原五边形的边,即由五条对角线围成的三角形,共有5+5=10个

由分类计数原理得,不同的三角形共有5+20+10=35个.

例5 75600有多少个正约数?有多少个奇约数?

解:75600的约数就是能整除75600的整数,所以本题就是分别求能整除75600的整数和奇约数的个数.  

由于 75600=2⁴×3³×5²×7

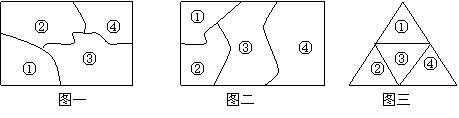
若变为图二,图三呢?(240种,5×4×4×4=320种)

例4 如下图,共有多少个不同的三角形?

解:所有不同的三角形可分为三类”