
∵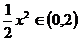 ,∴
,∴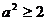 ,即
,即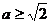 ,
,
又∵
(2)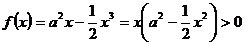 在
在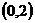 上恒成立,即
上恒成立,即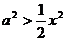 在
在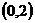 上恒成立,
上恒成立,
解:(1)若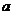 、
、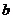 、
、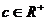 ,则
,则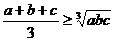 (当且仅当
(当且仅当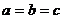 时取等号)。
时取等号)。
(3)对满足(2)的条件的一个常数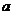 ,设
,设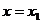 时,
时,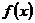 取得最大值。试构造一个定义在
取得最大值。试构造一个定义在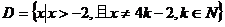 上的函数
上的函数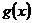 ,使当
,使当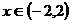 时,
时,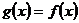 ,当
,当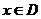 时,
时,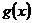 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以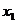 为首项的等差数列。
为首项的等差数列。
(2)若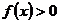 在
在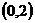 上恒成立,且函数
上恒成立,且函数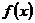 的最大值大于
的最大值大于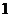 ,求实数
,求实数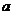 的取值范围,并由此猜测
的取值范围,并由此猜测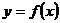 的单调性(无需证明);
的单调性(无需证明);
(1)可以证明:定理“若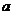 、
、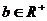 ,则
,则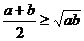 (当且仅当
(当且仅当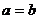 时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
13. (理)已知
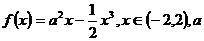 为正常数。
为正常数。
(2)一个解集为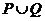 的不等式可以是
的不等式可以是 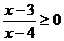 。
。
∴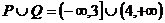 。
。
又不等式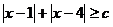 对任意
对任意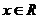 恒成立,∴
恒成立,∴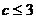 ,即
,即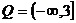 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com