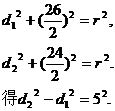
根据点到直线的距离公式，得

                   L₂         

                       L₁    

               M              

     O                 X      

点M到L₁，L₂的距离分别为d₁,d₂

根据弦、弦心距、半径三者之间的关系，有

      Y                       

（1983年文科第九题）如图，已知两条直线L₁:2x-3y+2=0,L₂:3x-2y+3=0.有一动圆（圆心和半径都在变动）与L₁，L₂都相交，并且L₁，L₂被截在圆内的两条线段的长度分别是定值26，24求圆心M的轨迹方程，并说出轨迹的名称

解：设圆心M的坐标为(x,y)，圆的半径为r，

解：选取AB所在直线为横轴，从A到B为正方向，以AB中点O为原点，过O作AB的垂线为纵轴，则A为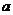（-，0），B为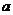（，0），设P为（x,y)

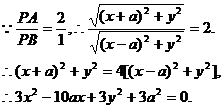
因为x²,y²两项的系数相等，且缺xy项，所以轨迹的图形是圆

    （1982年文科第七题）已知定点A，B且AB=2，如果动点P到点A的距离和到点B的距离之比为2∶1，求点P的轨迹方程，并说明它表示什么曲线

∵0＜α＜π,∴等号成立当且仅当cosα-=0 即α=60⁰

【评析】这些该题本身不难，但三角证明题出现证法太多，标准不易统一，给阅卷带来非常大的难度。另一方面，这一答案给出的分析法证明格式也不对，一般分析法证明题格式“要证A，只要证B”形式，B是A的充分不必要条件即可，而不是由A导出B。

（1+cosα)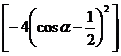≤0∴不等式得证

所以问题又化为证明不等式 (1+cosα)[4(1-cosα)cosα-1]≤0

解：即证：两端乘以sinα，问题化为证明2sinαsin2α≤1+cosα.而 2sinαsin2α=4sinαcos²α=4(1-cos²α)cosα=4(1-cosα)(1+cosα)cosα