
A,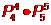 B,
B,
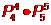 C,
C,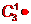
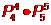 D,
D,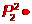
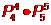
【答】D
【评析】这种排列组合用符号表示的试题在全国1988年已经有了不宜出的结论,它再次重蹈了历史覆辙。
DF=DC?sinC=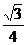 ,CF=DC?cosC=
,CF=DC?cosC= .取BC中点G.∵EB=EC,∴EG⊥BC.在Rt△BEF中,EF2=BF?GF,又BF=BC-FC=
.取BC中点G.∵EB=EC,∴EG⊥BC.在Rt△BEF中,EF2=BF?GF,又BF=BC-FC=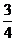 ,GF=
,GF= ,∴EF2=
,∴EF2=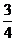 ?
? ,即EF=
,即EF=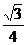 .∴tg∠DEF=
.∴tg∠DEF= .∴∠DEF=45°.故二面角α为45°.
.∴∠DEF=45°.故二面角α为45°.
(1994年上海18)计划在某画廊展出10幅不同的画,其中1幅水彩画、4幅油画、5幅国画,排列一行陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端,那么不同的陈列方式有( )种
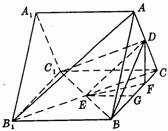
(2)解:作DF⊥BC,垂足为F,则DF⊥面B1BCC1,连结EF,则EF是ED在平面B1BCC1上的射影.∵AB1⊥BC1,由(1)知AB1∥DE,∴DE⊥BC1,则BC1⊥EF,∴∠DEF是二面角α的平面角.设AC=1,则DC= .∵△ABC是正三角形,∴在Rt△DCF中,
.∵△ABC是正三角形,∴在Rt△DCF中,
 【解答】(1)证明:∵A1B
【解答】(1)证明:∵A1B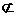 平面DBC1,DE
平面DBC1,DE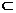 平面DBC1,∴AB1∥平面DBC1.
平面DBC1,∴AB1∥平面DBC1.
(1991年三南高考数学第24题)设函数f(x)=x2+x+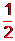 的定义域是[n,n+1](n是自然数),那么在f(x)的值域中共有_____________个整数
的定义域是[n,n+1](n是自然数),那么在f(x)的值域中共有_____________个整数
【答案】2n+2
【评析】这是当年希望杯数学竞赛的一道数学试题,在高考中出现而且仍然以填空题出现,有照抄之嫌。
(1992年三南第14题)设数列{an}是正数组成的等比数列,公比q=2,a
A,210
B,
【答】B
【评析】该题运算量比较大,也是希望杯竞赛中一个非常类似的题,在还没有将运算能力当作一种能力考查时,出此题显然违背了考查“双基”的初衷。
【说明】该阶段,高考内容上以《考试说明》为准绳,目的逐步变化成“为大学选拔新生服务的选拔性能力考试”,命题的人员也逐步变化为以高校为主,出台了许多量化指标,该阶段的败题,主要体现为预估难度(考试说明的规定难度)与实际难度(实际分数)不符,这一原因现在多数专家认为是高校教师不了解中学教学的实际所致。
(1994年全国理文23题)如图,已知A1B
(1)证明AB1∥平面DBC1;(2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数.
当n为偶数时,原不等式的解集是{x|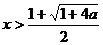 }
}
【评析】该题照搬了当年湖北黄冈、河北辛集中学及北京海淀区的模拟试题,包括数值都没有变化。
综合得:当n为奇数时,原不等式的解集是{x|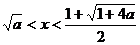 };
};
所以,不等式③的解集为{x|x> }.
}.
因为a>1,③式等价于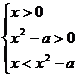

 或
或 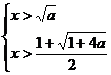 因为
因为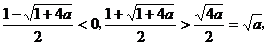
当n为偶数时, <0,不等式①等价于logax>loga(x2-a).
③
<0,不等式①等价于logax>loga(x2-a).
③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com