，所以5d²=│a－2b│² =a²+4b²－4ab ≥a²+4b²－2(a²+b²) =2b²－a²=1，

当且仅当a=b时上式等号成立，此时5d²=1，从而d取得最小值．

从而得2b²－a²=1．又点P(a，b)到直线x－2y=0的距离为

【解析】解法一:设圆的圆心为P(a，b)，半径为r，则点P到x轴，y轴的距离分别为│b│，  │a│．由题设知圆P截x轴所得劣弧对的圆心角为90°，知圆P截X轴所得的弦长为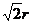，故r²=2b²，又圆P截y轴所得的弦长为2，所以有r²=a²+1．

【评析】该题就某一知识进行了加深，竞赛味道过于浓厚。实际难度为0.09,也属于废题。

（1997年全国理25）设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3:1，在满足条件①、②的所有圆中，求圆心到直线l:x-2y=0的距离最小的圆的方程．

因为ax₂<1，所以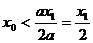

∴，

(Ⅱ)依题意知

因为x₁，x₂是方程f(x)－x=0的根，即x₁，x₂是方程ax²+(b－1)x+c=0的根．

得  x₁－f(x)>0．由此得f(x)<x₁．

因为所以x₁－x>0，1+a(x－x₂)=1+ax－ax₂>1－ax₂>0．

即x<f(x)．