
A.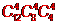 种B.
种B.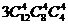 种 C.
种 C. 种 D.
种 D. 种
种
【解答】A
【评析】这是重蹈历史覆辙不该以这种形式出现的题。每换一帮人出题,总会出现这种重蹈历史覆辙的情况。
【说明】该阶段试题以省市为主的自主招生为主,并逐步向“高校自主招生试题”转移,以《考试大纲》代替了原来的《考试说明》,这一阶段的败题主要体现为“不严密”或“考察意图失落”
【评析】这一题,许多文科生没有读懂就下手做,预估文理课差不多的情况,但实际是文科难度为0.175,区分度为0.097.,大多数文科生不会。在分析报告种,再度强调了“要体现文理科的差异”。
(2001年上海11)已知两个圆:x2+y2=1①与x2+(y-3)2=1②,则又①式减去②式可得上述两圆的对称轴方程.将上述命题在曲线的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例,推广的命题为 .
【解答】设圆方程(x-a)2+(y-b)2=r2 ① (x-c)2+(y-d)2=r2 ②(a≠c或b≠d),由①-②,得两圆的对称轴方程.
【解析】这是1999年类比的延续试验,该题基本上白送分,没有区分度。
(2002年北京理9)12名同学分别到三个不同的路口进行车流量的调查,若每个路口4人,则不同的分配方案共有
【评析】该题命题从排列组合二项式定理同时以大题形式出现,考了冷门,当年《考试说明》排列组合的证明只是了解层次,预估难度0.5,实际则是0.141,区分度为0.464.之后形成定格:排列组合二项式定理以小题形式考,而且一般出此不出彼的格局;同时,也台出形成了“遵循考试说明(大纲),但有不拘泥于大纲的政策”。
(2001年理文科12,广东12天津山西江西12,)如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为 ( )
(A) 26
(B) 24
(C) 20
(D) 19
【解答】D
∴  .即 (1+m)n>(1+n)m.
.即 (1+m)n>(1+n)m.
又 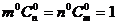 ,
, ,
, .
.
(Ⅱ)证明由二项式定理有 ,
,
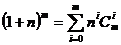 ,由 (Ⅰ)知
,由 (Ⅰ)知 >
>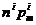 (1<i≤m<n),而
(1<i≤m<n),而 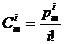 ,
, ,
所以,
,
所以,  (1<i≤m<n).因此,
(1<i≤m<n).因此,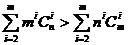 .
.
所以 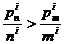 ,即
,即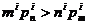 .
.
由于 m<n,对整数k = 1,2…,i-1,有 ,
,
【解答】(Ⅰ)证明: 对于1<i≤m有 = m?…?(m-i+1),
= m?…?(m-i+1),  …
… , 同理
, 同理  …
…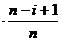 ,
,
(2001年全国理20) 已知i,m,n是正整数,且1<i≤m<n. (Ⅰ)证明 ;(Ⅱ)证明(1+m) n> (1+n) m.
;(Ⅱ)证明(1+m) n> (1+n) m.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com