13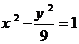．                  14．②③     

记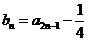，n＝l，2，3，…?．

（1）求a₂，a₃；（4分）

（2）判断数列{b_n}是否为等比数列，并证明你的结论；（7分）

嵩 明 一 中 高 三 年 级 数 学 测 试 卷 答 案

（理）

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

C

D

C

B

B

A

C

C

A

A

B

D

（文）

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

C

D

A

C

D

B

D

B

C

D

A

C

（理）

22．（11分）设数列{a_n}的首项a₁=a≠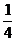，且  ,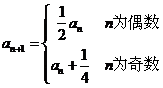

21．（11分）进货原价为80元的商品400个，按90元一个售出时，可全部卖出。已知这种商品每个涨价一元，其销售数就减少20个，问售价应为多少时所获得利润最大？

（2）求ED与平面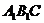所成角的大小；（5分）

（3）求二面角E-BD-C的大小．（5分）

（1）求证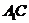：⊥平面EBD；(3分)

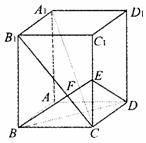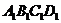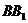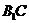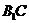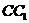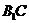20．（13分）已知长方体ABCD-中，棱AB＝BC＝3，＝4，连结，过B点作的垂线交于E，交于F．

19．（13分）直线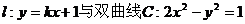的右支交于不同的两点A、B.

（1）求实数k的取值范围；（6分）

（2）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不存在，说明理由.（7分）

（文）甲、乙两人在罚球线投球命中的概率分别为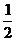与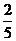

（1）甲、乙两人在罚球线各投球一次，求两人都没投中的概率；（5分）

（2）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率。（6分）

18．（11分）（理）甲、乙两人在罚球线投球命中的概率分别为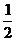与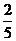，投中得1分，投不中得0分

（1）甲、乙两人在罚球线各投球一次，求两人得分之和x的数学期望；（5分）

（2）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率。（6分）