将其代入x²=2py，消去y整理得x²-2pkx-2p²=0.                                 

设A，B的坐标分别为A（x₁，y₁），B(x₂，y₂)，则x₁x₂=-2p².                     

20. （本小题满分12分）

（Ⅰ）解：依题意，直线l的斜率存在，设直线l的方程为y=kx+p，

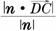∴点C到平面D₁DP的距离为d=        =.

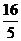则             即令x=-3,则y=4.  

∴n=(-3,4,0).  

∵P(4,3,4), ∴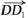=(0,0,4),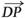=(4,3,4).

(Ⅲ) ∵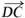=(0,4,0),设平面D₁DP的法向量n=(x,y,z),

∴CP与平面D₁DCC₁所成角的正弦值为.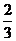

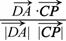∴cos<, >=          =.

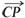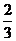∵AD⊥平面D₁DCC_1, ∴=(4,0,0)是平面D₁DCC₁的法向量. 

（Ⅱ）由题设可得,P（4,2,4），故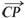=（4，-2，4）.