1、若函数f(x)为定义域为D的奇函数，则f(x)应满足：⑴对任意x∈D，都有      ；（或者说函数f(x)的定义域是           的区间）⑵f(－x)＝          ；若函数f(x)为定义域为D的偶函数，则f(x)应满足：⑴对任意x∈D，都有      ；⑵f(－x)＝          ；

3、奇偶性：奇函数、偶函数、又奇又偶、非奇非偶,要学会用图象判断函数的奇偶性

〖双基回顾〗

f(－x)＝f(x)Û f(－x)－f(x)＝0Û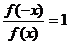( f(x)≠0)；

2、f(－x)＝－f(x)Û f(－x)＋f(x)＝0Û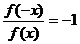( f(x)≠0)、

1、函数为奇函数或偶函数的必要条件是其定义域为关于原点对称的区间；

2.4  函数的奇偶性

〖考纲要求〗理解函数的奇偶性的概念，并能判定一些简单函数的奇偶性；理解奇函数和偶函数的图象的对称性，并能用对称性描绘奇函数或偶函数的图象.

〖复习要求〗会判断函数的奇偶性，能利用函数的奇偶性解决一些实际问题.

〖复习建议〗要正确理解函数的奇偶性的定义，奇偶函数的定义是判定函数奇偶性的根本依据，但要注意：

*9、=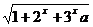在（－∞，1）有意义，求实数a的取值范围

⑵解不等式：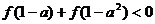

⑴求证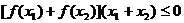：（提示：可分x₁＋x₂≥0与x₁＋x₂≤0证明）

8、y=是[－1，1]上的减函数，又是奇函数.