2、原函数的定义域是反函数的                ；原函数的值域是反函数的            .

1、求反函数的三个步骤是：⑴                    ⑵              ⑶              .

2.5  反函数

〖考纲要求〗掌握互相为反函数图象之间的关系.

〖复习要求〗理解反函数的概念，知道什么函数有反函数，会求一个函数的反函数，掌握互为反函数图象之间的关系.

〖复习建议〗记住求反函数的步骤，知道原函数与反函数的定义域、值域关系，图象关系，单调性关系，能利用反函数研究原函数的性质.

〖双基回顾〗

9、已知f(x)＝，如果 xg(x)＞0，求证：f(x)＞0.

  8、奇函数y=f(x)满足x<0时，f(x)=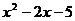，求函数y=f(x)的表达式并且解方程f(x)=2x.

7、如果函数y=f(x)是偶函数，y=g(x)是奇函数，且f(x)＋g(x)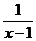＝，求f(x)与、g(x)的表达式.

（求证：函数y=f(x)的定义域关于原点对称，则y=f(x)一定可以表示为一个奇函数和一个偶函数之和）

 （1）f(x)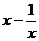＝；                           （2）；

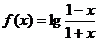6、判断下列函数的奇偶性：

5、已知f(x)＝ax²＋bx＋3a＋b是偶函数，且其定义域为[a－1，2a]，则a＝      、b＝       .

4、已知f(x)＝x⁵＋ax³＋bx－8，且f(－2)＝10，那么f(2)等于………………………………………（   ）

（A）－26        （B）－18              （C）－10           （D）10