（A）2.5m         （B）4m        （C）5m        （D）6m

2、如图，花坛水池中央有一喷泉，水管OP=1米，水从喷头P喷出后呈抛物线状，先向上至最高点后落下，如果最高点距离水面2米，P距离抛物线对称轴1米，则在水池直径的下列可选值中，最合算的是……………（    ）

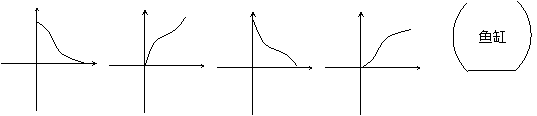1、一个高为H，水量为V的鱼缸的轴截面如图，其底部有一个洞，满缸水从洞中流出，如果水深为h时水的体积为v，则函数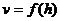的大致图象是……………………………………………（    ）

4、某工厂今年1、2、3月生产产品1万件、1.2万件、1.3万件，为了估计以后每个月的产量，以这三个月的产量为依据，用一个函数模拟该产品的月产量y与月份数x的关系，模拟函数可以选用二次函数或者函数y=a?b^x+c，如果已知4月份产量为1.37万件，问用以上哪一个函数模拟比较好，理由是什么？

3.某商场销售甲种商品所获利润P（万元）以及销售乙种商品所获利润Q（万元）与投入资金x（万元）的关系分别为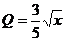，，现在该商场准备用3万元资金经营这两种商品.试问，应该对甲，乙两种商品分别投入多少资金，才能使经营这两种商品的总利润最大，并求这总利润是多少万元？.

(2)要使此项税收在税率调节后不低于原计划税收的83.2%，试确定x的取值范围.

2.政府收购某种农产品的原价格为每担200元，其中征税率标准为100元征10元（称税率为10个百分点，即10%），并计划收购a万担.为了减轻农民的负担，现决定将税率降低x个百分点，预计收购量可增加2x个百分点.

  (1)写出税收y与x的函数关系；

1.某商人如果将进货单价为8元的商品按每件10元售出时，每天可售出100件.现在他采用提高售出价，减少进货量的办法增加利润，已知这种商品每件提价1元，其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚得的利润最大？并求出最大利润..

2.10  函数应用问题

〖考纲要求〗会建立目标函数解决有关实际问题.

〖复习建议〗在熟练掌握一次函数、二次函数、幂函数、指数与对数函数的基础上，能把一些生活问题转化为对应的函数问题，并且能用不等式等数学知识解决具体的数学问题.