
(1)若a=(x1,y1),b=(x2,y2),则a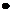 b=x1x2+y1y2;
b=x1x2+y1y2;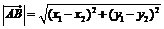 ;
;
5.平面向量数量积的坐标表示:
4.设A(x1,x2)、B(x2,y2),则SㄓAOB= ;
;
3.设a=(x1,y1),b=(x2,y2),则a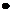 b=
b=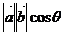 =x1x2+y1y2;其几何意义是a
=x1x2+y1y2;其几何意义是a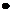 b等于a的长度与b在a的方向上的投影的乘积;
b等于a的长度与b在a的方向上的投影的乘积;
2.两个向量垂直的充要条件, 设a=(x1,y1),b=(x2,y2),
(1)向量式:a⊥b(b≠0)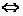 a
a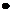 b=0; (2)坐标式:a⊥b
b=0; (2)坐标式:a⊥b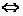 x1x2+y1y2=0;
x1x2+y1y2=0;
1.两个向量平行的充要条件,设a=(x1,y1),b=(x2,y2),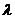 为实数。(1)向量式:a∥b(b≠0)
为实数。(1)向量式:a∥b(b≠0)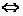 a=
a=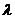 b;(2)坐标式:a∥b(b≠0)
b;(2)坐标式:a∥b(b≠0)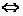 x1y2-x2y1=0;
x1y2-x2y1=0;
§5.4 向量的应用
〖复习要求〗理解向量的几何、代数、三角及物理方面的应用,能将当前问题转化为可用向量解决的问题,培养学生的创新精神和应用能力。
〖双基回顾〗
6、已知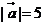 ,
,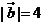 ,
, ,则
,则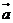 与
与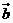 的夹角
的夹角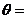 ______
______
5、
已知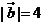 ,
,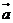 在
在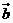 上的投影是
上的投影是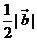 ,则
,则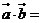 ______;
______;
4、 已知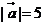 ,
,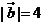 ,
,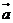 与
与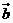 的夹角
的夹角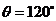 ,则
,则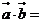 ______;
______;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com