①求向量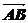的坐标；

②求圆x²－6x＋y²＋2y=0关于直线OB对称的圆的方程；

③是否存在实数a，使得抛物线y=ax²－1上的点总有关于直线OB对称的两个点？如果有，求出a的取值范围，如果不存在，说明理由！

〖课堂练习〗

3、（2003年上海高考题，16分=4分＋5分＋7分）在以O为原点的直角坐标系中，A（4，－3）为直角三角形OAB的直角顶点，已知|AB|=2|OA|，并且点B的纵坐标大于零.

  2、如抛物线y=x²＋3x－1上存在两个不同点关于直线x＋y=0对称，求出这两个点的坐标.

  1、求抛物线C：y²－2x－4y＋6=0关于下列元素的对称曲线：

⑴点（0，1）；

⑵直线x＋y－1=0；

  4、设曲线xy=1与⊙C：x²＋y²－4x－4y＋3=0交于A、B两点，则AB的中垂线方程为             .

〖例题分析〗

  3、⊙C：x²＋y²＋4x－12y＋39=0关于直线l：3x＋my－12=0对称，则实数m=         ；

  2、曲线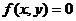关于直线y=x+b对称曲线方程为             ；

  1、点A（a，0）、B（4，b）关于点C（2，3）对称，则a=         ；b=        ；

7、抛物线y²=x＋1，定点A（3，1），B是抛物线上任意一点，点P在AB上满足BP：PA=1：2，当点B在抛物线上运动时，求点P的轨迹方程并指出轨迹是什么曲线？

圆锥曲线中的对称问题

〖考试内容〗理解中心对称和轴对称的概念，掌握求点和曲线关于直线的对称点或者对称曲线的一般方法，熟练掌握几种特殊曲线的对称问题.

〖复习要求〗掌握中心对称的实质――中点问题；轴对称的实质――中点与斜率问题；掌握点关于点、原点、x轴、y轴、直线y=±x＋m、x=a、y=b的对称点.

〖知识点训练〗

（A）0个             （B）1个             （C）2个             （D）3个
6、△ABC中，三边a、b、c成等差数列，A(－1,0)、C(1,0)，则顶点B的轨迹方程为              .