
(Ⅱ)因为b2=1, bn+2- b =(bn+1-2n)(bn+1+2n+1)-
b
=(bn+1-2n)(bn+1+2n+1)-
b =2n+1?bn-1-2n?bn+1-2n?2n+1=2n(bn+1-2n+1)
=2n+1?bn-1-2n?bn+1-2n?2n+1=2n(bn+1-2n+1)
=2n(bn+2n-2n+1)=2n(bn-2n)=…=2n(b1-2)=-2n〈0,所以bn-bn+2<b2n+1
所以bn?bn+2<b , ……………12分
, ……………12分
解法二:(Ⅰ)同解法一.
因为bn?bn+2-b =(2n-1)(2n+2-1)-(2n-1-1)2=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)=-5?2n+4?2n=-2n<0,
=(2n-1)(2n+2-1)-(2n-1-1)2=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)=-5?2n+4?2n=-2n<0,
bn=(bn-bn-1)+(bn-1-bn-2)+???+(b2-b1)+b1=2n-1+2n-2+???+2+1=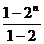
19.解: (Ⅰ)由已知得an+1=an+1、即an+1-an=1, ……………………2分
又a1=1,所以数列{an}是以1为首项,公差为1的等差数列.故an=1+(a-1)×1=n.
(Ⅱ) 由(Ⅰ)知:an=n从而bn+1-bn=2n.
(Ⅰ)求数列{an}的通项公式;(Ⅱ)若列数{bn}满足b1=1,bn+1=bn+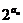 ,求证:bn
,求证:bn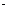 bn+2<b2n+1.
bn+2<b2n+1.
已知{an}是正数组成的数列,a1=1,且点( )(n
)(n N*)在函数y=x2+1的图象上.
N*)在函数y=x2+1的图象上.
19.(本小题满分12分)
联立方程组 解得
解得 ,
,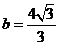 所以
所以 的面积
的面积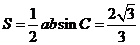
(Ⅱ)由正弦定理,已知条件化为 ,?????????????????????????????????????????????????????? 8分
,?????????????????????????????????????????????????????? 8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com