
1、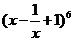 展开式中的常数项是……………………………………………………( ).
展开式中的常数项是……………………………………………………( ).
(A)1 (B)40 (C)41 (D)39
6、通项公式及其应用是复习二项式定理的基本问题,要达到熟练的程度;
【课堂练习】
1、要正确理解二项式定理,准确地写出二项式的展开式;2、要注意区分项的系数与项的二项式系数;3、要注意二项式定理在近似计算及证明整除性中的应用。4、求系数和或部分系数和时,通常用赋值法;5、运用系数最大值性质时应注意区分n是偶数还是奇数;
例6、若n为奇数,求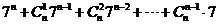 被9除的余数。
被9除的余数。
【课堂小结】
例5、求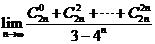
(3)|a0|+|a1|+|a2|+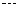 +|a8|的值.
+|a8|的值.
(1)a1+a2+ a8的值
a8的值
(2)a2+a4+a6+a8的值
例4、设(2-x)8=a0+a1x+a2x2+ +a8x8,求:
+a8x8,求:
例3、已知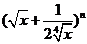 展开式中前3项的系数成等差数列,求展开式中x的整数次幂项.
展开式中前3项的系数成等差数列,求展开式中x的整数次幂项.
例2、若(1+2x)n中第6项与第8项的二项式系数相等,求按升幂排列的前3项。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com