3．理解掌握用欧姆定律分析实际问题，解释实际问题。

2．掌握欧姆定律计算有关问题。

1．理解掌握部分电路欧姆定律及其表达式。

　如果你的收音机不响了，检查后发现有一个200欧姆的电阻烧坏了，需要更换. 但是你手边又只有一个100欧和几个50欧的电阻，能否用它们组合起来，使组合的电阻相当于一个200欧的电阻呢？学习了电阻的串联的知识后，你就会知道这种等效替换是容易实现的。

　把电阻一个接一个地连接起来，就叫电阻的串联. 我们可以通过实验来找出串联电路的总电阻跟各个串联电阻的关系。为此我们先要根据欧姆定律，用伏安法测出每一个电阻的阻值，再测串联电路的总电阻值。

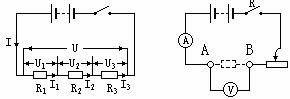
　　　　　　　　　　　　　　 图6　　　　　　　　　 图7

　分别先后将2欧、3欧、5欧定值电阻接于图7的A、B之间，测算其阻值。

　撤去5欧电阻时，不移动变阻器滑动片的位置，把2欧和3欧电阻串联起来接于A、B之间，发现电流表和电压表的读数跟接5欧电阻时相同. 这就说明，2欧和3欧电阻串联后的等效电阻(总电阻)为5欧。

再换用其它阻值的电阻，所得到的结果一样.刚才的实验不仅得出了串联电路的总电阻等于各串联电阻之和，而且还看到，当用2欧、3欧电阻串联后去代替5欧电阻，电路中的电流、电压跟接5欧电阻时一样。这就是说用2、3欧的串联电阻替换5欧电阻时，没有改变电路的电流、电压效果。所以常常把串联电路的总电阻叫做等效电阻，即这个串联电路等效于一个阻值为一定的电阻。用几个电阻联成电路去等效替换一个电阻，或用一个电阻去等效替换一个电路的方法叫等效替换法。

把几个电阻串联起来后，相当于增加了导体的长度，所以总电阻比几个串联电阻中最大的那个还大。

刚才实验得出的电阻关系还可以运用我们已学过的欧姆定律及关于串联电路的电流和电压知识推导出来。先在电路图(图6)上把各个电阻和整个电路的电流、电压用下标区别标志出来. 应用欧姆定律于串联电路和每一个电阻，得

　电阻关系式的推导：由I=U／R，U=IR

　分别对串联电路和各个电阻得

　U=IR，U₁=I₁R₁，U₂=I₂R₂，U₃=I₃R₃ (1)

　根据前面学到的串联电路中的电流关系和电压关系的知识可知

　I=I₁=I₂=I₃ (2)

　U=U₁+U₂+U₃ (3)

　∴ IR=IR₁+IR₂+IR₃

　R=R₁+R₂+R₃ (4)

(4)式与实验结论一致。推导的根据是欧姆定律和串联电路的电流、电压特点，这也是我们解串联电路时的根据。从推导中看到，欧姆定律既可用于各个导体，也可能用于整个电路. 这时要注意各个电阻的U、I、R要用不同的下标区别，且同一电阻的U、I、R要用相同的下标，以正确表达欧姆定律公式中各量是同一导体的量，解电路时这样“下标配套”是避免出现“张冠李戴”的错误的好措施。

根据上述规律，如果是n个阻值均为R的电阻串联后，总电阻R_总=nR。

　另外由于在串联电路中：I₁=I₂，

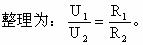
这说明在串联电路中，电阻有分压作用，而且电压的分配与电阻成正比.这是很有价值的一条规律.

　　 如果一个用电器的一个10欧的电阻坏了，可是手头却只有几个20欧的电阻.能不能用几个20欧的电阻来替代一个10欧电阻呢？同学们可能会想到并联.

我们来看一个实验，步骤如下：先按图8将R_l=10欧、R₂=15欧组成并联电路，闭合电键，记下电流表和电压表的示数.然后用阻值为6欧的电阻取代并联的两电阻R₁和R₂。闭合电键，我们发现电流表与电压表的示数与刚才一样。

　 根据两次实验中电流表、电压表的示数完全相同这一事实，可称电阻R是并联电阻R₁、R₂的并联等效电阻。

　实验中并联电阻R₁、R₂的阻值分别为10欧和15欧，而它们的等效电阻只有6欧。为什么并联电阻后总电阻值变小呢？并联电路中总电阻与分电阻间关系满足什么数学规律呢？　

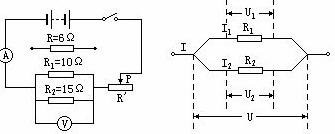
图8　　　　　　　　　　　　 图9

　这一关系仍然是利用实验规律加数学推导而得出的，下面以两个电阻的并联为例来推导这一关系，如图9所示。

　设电阻R₁与R₂并联时，总电阻为R.

　因为，并联电路中、干路中的电流等于各支路中的电流之和，即

　I=I₁+I₂ (1)

并联电路里，各支路两端的电压都相等，即

　U=U₁=U₂ (2)

　用(1)式除以(2)式得　

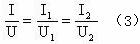
　所以，根据欧姆定律的变形式可知(3)式为

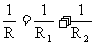
此式为并联电路等效电阻的计算式，它反映了电阻并联时，总电阻与分电阻间的关系。

　(1)式中R、R₁和R₂分别代表并联总电阻和两个分电阻。

　这时并联电路中的电阻关系可以表述为：并联电路的总电阻的倒数，等于各并联电阻的倒数之和。

　对并联电路电阻的关系作几点说明。

　(1)当n个电阻并联时，电阻关系的表达式应写成：

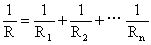
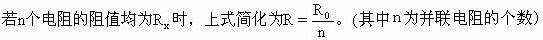
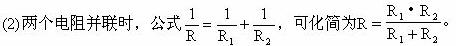
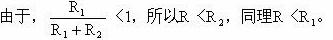
这表明两电阻并联后，总电阻比两个分电阻值中任何一个都小。

其实，任意多个电阻并联时，总电阻一定小于它们中阻值最小的电阻。

并联电阻后总电阻减少，这相当于增大了导体的横截面积。

由于L₁、L₂是并联，有：U₁=U₂

　根据欧姆定律得：I_lR_l=I₂R₂

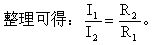
表明：在并联电路中电流的分配跟电阻成反比.这也是一条重要的规律。

　　 (1)内容

　由实验我们已知道了在电阻一定时，导体中的电流跟这段导体两端的电压成正比，在电压不变的情况下，导体中的电流跟导体的电阻成反比.把以上实验结果综合起来得出结论，即欧姆定律。

　导体中的电流跟导体两端的电压成正比，跟导体的电阻成反比。

欧姆定律是德国物理学家欧姆在19世纪初期(1827年)经过大量实验得出的一条关于电路的重要定律.后人为了纪念他的贡献，把电阻的单位和上述电流定律都用他的名字命名。

欧姆定律的公式：如果用U表示加在导体两端的电压，R表示这段导体的电阻，I表示这段导体中的电流，那么，欧姆定律可以写成如下公式：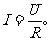

这个公式是怎样概括表述了欧姆定律的内容呢？我们以导体电阻R一定的情况来说明，若导体两端的电压由U₁变为U₂时，流过导体电流由I₁变为I₂，则由欧姆定律写出下面两式，并将两式相除，即得到：在电阻一定时，流过导体的电流与导体两端的电压成正比。

　R一定时，I₁=U₁／R　I₂=U₂／R　

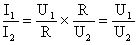
　如果导体两端的电压一定，它的电阻由R₁变为R₂时，电流由I₁变为I₂. 则由欧姆定律写出下面两式，并将两式相除，即得到：在电压一定时，流过导体的电流与导体的电阻成反比。

　U一定时，I₁=U／R₁　 I₂=U／R₂　

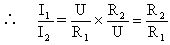
　大家看到，欧姆定律的内容和公式都简洁优美地概括了前面一定条件下由实验得出的结论。而且从欧姆定律的公式我们可以看到，只要知道了导体的电阻值和它两端的电压，就可求出导体中的电流。所以欧姆定律更全面地反映了导体中电流、电压和电阻的关系。

　公式中I、U、R的单位分别是安、伏和欧。

公式的物理意义：当导体的电阻R一定时，导体两端的电压增加几倍，通过这段导体的电流就增加几倍.这反映导体的电阻一定时，导体中的电流跟导体两端的电压成正比例关系(I∝U).当电压一定时，导体的电阻增加到原来的几倍，则导体中的电流就减小为原来的几分之一.反映了电压一定时，导体中的电流跟导体的电阻成反比例的关系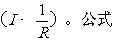

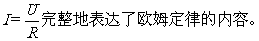
　有关欧姆定律的几点说明：

　①欧姆定律中的电流、电压和电阻这三个量是对同一段导体而言的.

　②对于一段电路，只要知道I、U和R三个物理量中的两个，就可以应用欧姆定律求出另一个。

③使用公式进行计算时，各物理量要用所要求的单位。

④欧姆定律中的电流、电压和电阻这三个量是对同一段导体的同一时刻而言的

(2)应用欧姆定律计算有关电流、电压和电阻的简单问题。

应用欧姆定律计算电路问题的一般步骤：

　(1)读题、审题。

　(2)根据题意画出完整的电路图或某一段电路的示意图。

　(3)在图上标明已知量的符号、数值和未知量的符号。

(4)选用物理公式进行计算(书写格式要完整，规范) 。

　例1. 一盏白炽电灯，电阻为807欧，接在220伏的电源上，如图3所示，求通过这盏电灯的电流。

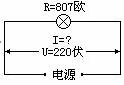
图3

解题步骤：

　已知：R=807欧 U=220伏

　求：I=？　

解：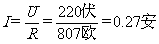

　答：通过白炽电灯的电流约为0.27安。

例2. 如图4所示，有一种指示灯，电阻为6.3欧，通过的电流为0.45安时才能正常发光.要使这种指示灯正常发光，应加多大的电压？

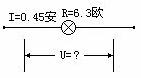
图4

解题步骤：

　已知：R=6.3欧 I=0.45安

求：U=？

解：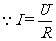

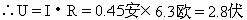
　答：要使这种指示灯正常发光，应加大约2.8伏的电压.

例3. 用电压表测出一段导体两端的电压是7.2伏，用安培计测出通过这段导体的电流为0.4安，求这段导体的电阻。

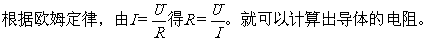
由例题3可知，欧姆定律为人们提供了一种测定导体电阻大小的方法，这种方法叫伏安法.

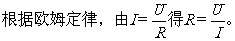　所以只要用伏特表测出导体两端的电压和用安培表测出流过导体的电流，就可以计算出导体的电阻.

　实验电路：

图5

步骤：

　①按电路图连接电路.连接电路时开关应是断开状态.滑动变阻器的滑片要放在最大电阻值位置.电压表和电流表的正负接线柱要连接正确.电压表使用0-3伏量程，电流表使用0-0.6安量程。

　②检查电路连接无误后，闭合开关；调节滑动变阻器的滑片，改变被测电阻两端的电压，观察电压表的示数为l伏、2伏和3伏时电流表的读数；将三组电压和电流的对应值填入自己设计的实验记录表格中。

　③根据记录的三组实验数据分别算出未知电阻的三个值.为了减小误差，算出电阻的平均值，作为被测电阻的阻值.即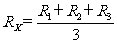

(二)电流与电阻的关系

电路图同上，换用不同阻值的定值电阻，调节滑动变阻器滑动触头，使电压表读数保持不变，将定值电阻值和对应的电流表读数填入表格。

表格(U=3V)

结论：电阻R两端的电压一定时，流过R的电流跟电阻R的阻值成反比。”

(一)电流与电压的关系

1. 按下图2所示的电路图连接实验电路.先不连电压表，看清回路：电流表与R串联.读数表示通过R的电流.然后再将电压表接入，看清：电压表与R并联，读数表示R两端的电压。

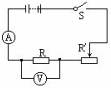
图2

2. 闭合开关，调节滑动变阻器的滑动触头，使R两端电压成整数倍地变化，同时将电流表和电压表的读数填入表格中。

表格(R=5Ω)

结论：电阻R一定时，流过R的电流跟R两端的电压成正比.

在前面我们分别学习了电流、电压、电阻的概念.我们已经知道电荷的定向移动才会形成电流，导体两端有电压电荷才会定向移动。

一方面，电压是产生电流的原因，导体两端有电压，导体中才会有电流.可以猜想：所加电压越高，电流就会越大。

　另一方面，任何导体都有电阻，电阻就是导体对电流的阻碍作用.可以推断：导体电阻越大，电流就越小。

即通过导体的电流的大小可能与导体两端的电压和导体的电阻这两个因素有关系. 下面我们利用实验来看一下。所需的器材有：干电池2节、滑动变阻器、2.5伏小灯泡、开关、导线。

步骤：

1. 按图1连接电路，改变滑动片的位置，观察电灯的亮度变化。

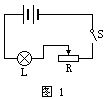
　当灯泡最暗时，此时滑动片在左端，变阻器接入电路的电阻最大，通过灯泡的电流最小.

　2. 固定滑片位置不动，改变电池节数，观察电灯泡的亮度变化，用一节电池时，灯的亮度比用2节电池时的灯的亮度小，通过灯泡的电流小。

　结论：步骤1说明导体中的电流大小与导体中的电阻大小有关，电阻越大，电流越小.

　步骤2说明导体中的电流大小还与导体两端的电压大小有关，电压越高，电流越大.

　我们对于一个物理现象的研究，不应满足于“变大”、“变小”这种初步认识，还要进一步探索研究，就是说要知道电流与电压、电阻之间的定量关系.这就是我们本周研究的课题。

　我们通过做实验来研究，因为物理学是一门实验科学，通过物理实验可以使我们找到规律。

　电流可能受到两个因素电压、电阻的影响，如果电压、电阻同时变化，它们各自对电流的影响有互相加强或减弱的可能，也有互相抵消的可能，使我们无法判断电流与电压、电阻之间到底有什么关系.怎样设计实验呢？其实，一个量受几个因素影响的问题，前面的学习已经遇到过了.我们应用的就是变量控制法。

　我们如何来研究电流跟电压、电阻两个量的关系，应该“固定电阻，单独研究电流跟电压的关系”，或“固定电压，单独研究电流跟电阻的关系” 。这种把一个多因素的问题转变成为多个单因素问题的研究方法是实验物理中极为有用的方法。

2．电流与电阻的关系--电压一定时，电流与电阻成反比．

1．电流跟电压的关系--电阻一定时，电流与电压成正比．