1．有用功、额外功和总功

(1)定义

从字面上理解，“有用功”“额外功”“总功”的意思分别是：有用的功，额外的功和总共做的功，是这样吗？我们举个例子来分析一下．

如果让你把重100 N的砂子运上三楼，你会想到哪些方法？

如图14-13所示，你可以采取图中甲、乙、丙所表现的三种方法．

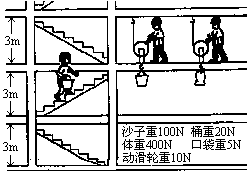
甲　　　　　　 乙　　　 丙

图14-13

甲是将砂子装入桶中，由人提桶上三楼，达到运送目的．在此过程中，你做了哪些功？有对砂子做的功、有对桶做的功和对你自己做的功．

乙是将砂子装入桶中，在三楼安装一个动滑轮，人站在三楼上，用动滑轮将装砂的桶提上三楼．在这个方法中，你做了哪些功？有对砂子做的功、有对桶做的功和对动滑轮做的功．

丙中是将砂子放入袋子中，同样用动滑轮将袋子提到三楼．在这种方法中，你做了哪些功？有对砂子做的功，有对袋子做的功和对动滑轮做的功．

分析完了，我们将甲、乙、丙三种方法做的功进行比较：

甲：W_砂、W_桶、W_人　　　　 乙：W_砂、W_桶、W_动　　　　 丙：W_砂、W_袋、W_动

在上表中不难看出，三种方法中都对砂子做了功，而且也只有这一项功是三种方法都做了的，其实这也是我们所需要完成的任务．这样做的功叫有用功．除W_砂之外，每种方法中还有W_桶、W_人、W_动、W_袋，但每种都不完全相同，这与我们采用的方法有关系，这些都是为完成目的不得不额外做的功．说到这里，你可能有疑问：能不能不出现这些额外做的功？那么，你能想出不用额外做功，直接将砂子“弄”上三楼的方法吗？没有吧，这样的方法是不存在的，或者说不论用什么方法达到目的，都会不得不额外做些．我们将这些额外负担所不得不做的功叫额外功．

每做一次功时，有用功与额外功之和就是总功．

根据上述定义，我们将图14-13的甲、乙、丙三种方法中做的功分列成：

甲：W_有用=W_砂　　　 W_额外=W_桶+W_人　　　　 W_总=W_砂+W_桶+W_人

乙：W_有用=W_砂　　　 W_额外=W_桶+W_动　　　　 W_总=W_砂+W_桶+W_动

丙：W_有用=W_砂　　　 W_额外=W_袋+W_动　　　　 W_总=W_砂+W_袋+W_动

再来看个例子：起重机如果由电动机带动，总功在数量上就等于实际消耗的能，有用功只是起重机将物体抬高时所做的功，而那些克服摩擦所消耗的能就属于额外功了．

你能再举出一个例子，说明哪些是有用功，哪些是额外功吗？自己试一试．

(2)三者的关系

由上述定义，我们可以看出有用功、额外功和总功三者的关系为：W_总=W_有用+W_额外

即总功等于有用功和额外功之和．而额外功是不得不做的功．因此，下列关系也总是成立：W_总＞W_有用

这两个关系是纯粹的数学关系，很好理解．

4．通过实验探究，养成与同学合作交流的意识以及创新意识．

[基础知识精讲]

在日常生活中，会出现很多对物体做功的情况，虽然达到了相同的目的，但做功的过程有时是不相同的．其实不仅是采用的形式不同，里面还有很多东西是有差别的，学过了今天的知识，你就会明白了．

3．探究测定几种简单机械的机械效率，能测定某种简单机械的机械效率，形成研究问题的方法；

1．了解有用功、额外功、总功的概念；　　 2．理解机械效率的公式，会做简单的计算；

⒈实验方法：

⒉测算方法：

第一步，表盘每转一圈电流所做的功：

W₀=3.6×10⁶/3000J=1.2×10³J。

第二步，在时间t内表盘转n圈所做的功：

W=nW₀= n×1.2×10³(J)。

第三步，用电器工作时的电功率P

P=W/t= n×1.2×10³/t(W)

⒈实验目的：测定小灯泡的额定功率和小灯泡不在额定电压下的实际功率。 ⒉实验原理：P=UI

⒊实验电路图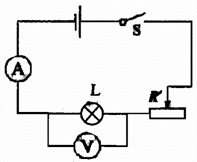： ⒋实验器材：

⒌实验数据记录表：

2．功的计算

知道了力在什么情况下才对物体做功，我们来看看功的大小如何计算．

在第十二章第5节我们已经看到，使用动滑轮时，当只有一个动滑轮绕过绳子，如图14-12所示，由于有两条绳子承担着物体的重量，实际的拉力只有物重的二分之一，但使物体上升h高度时，拉力作用点移动的距离是这一高度的两倍，为2h．如果你直接用手把重G的物体匀速提升h高度，与前一过程相比虽有不同之处，但你想一想有没有不变的量？

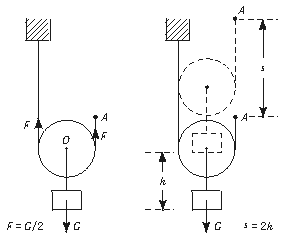
图14-12

我们发现，作用在重物G上的力和重物G移动距离的乘积在这两个过程中是相等的．

实际上，我们知道功的两个要素是作用在物体上的力和物体在力的方向上移动的距离．在物理学中，上述二者的乘积就是功．因此，功=力×力的方向上移动的距离．

我们分别用W、F、s代表功、力和力的方向上移动的距离，那么上述公式写成：

W=F·s

力、距离的单位分别是N、m，功的单位我们也已经学习过了，为焦耳，符号为J．

知道了功的计算公式了，我们来做几道简单的计算题吧．

例1．小明用50 N的水平推力在地面上推重100 N的箱子，前进10 m，小明做了多少功？

解：箱子受重力G和水平推力F，是箱子在水平方向上移动距离s，很显然，G与s方向垂直，G不做功，F与s方向一致，F是做功的力．

F=(　　 )，s=(　　 )

W=(　　 )=50 N×10 m=500(　　 )．

这道题的关键是找出做功的力，千万不能用W=Gs求功，那就大错特错了．

例2．上题中小明把箱子匀速举高150 cm，则做了多少功？

解：举力F做功，因为它的方向与物体上升高度方向相同，由于箱子匀速上升，所以F与G大小相等．

F=G=(　　 ) N，s=h=150 cm=(　　 )m

W=Fs=(　　 )×(　　 )=150 J

这两道题你会做了吗？主要是要你学会分析哪个力做了功，做简单的计算．

5．培养分析问题的能力、理论联系实际的能力．

[基础知识精讲]

你还记得在学习第十三章的知识时，我们发现使用机械时，省力的机械总是费距离，费力的机械却可以省距离，但无论如何我们也无法找到既省力又省距离的机械，你是否有疑问呢？想知道这是为什么吗？学习了本节的内容我们就知道了．

我们先从最基本的知识学起．